TRẮC NGHIỆM

Câu 1: Một hộp có 20 chiếc thẻ cùng loại, trong đó có 2 chiếc thẻ màu xanh và 18 chiếc thẻ màu trắng. Bạn Châu rút thẻ hai lần một cách ngẫu nhiên, mỗi lần rút một thẻ và thẻ được rút ra không bỏ lại hộp. Tính xác suất để cả hai lần bạn Châu đều rút được thẻ màu xanh.

• A.
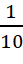
• B.

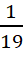
• C.

• D.

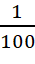
Câu 2: Trước khi đưa ra thị trường một sản phẩm, công ty phỏng vấn 800 khách hàng và được kết quả là 550 người nói sẽ mua, còn 250 người nói sẽ không mua. Theo kinh nghiệm của nhà sản xuất thì trong những người nói sẽ mua sẽ có 60% số người chắc chắn mua, còn trong những người nói sẽ không mua lại có 1% người chắc chắn mua. Chọn ngẫu nhiên một khách hàng. Xác suất chọn được khách hàng chắc chắn mua là bao nhiêu?

• A.

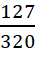
• B.

• C.
• D.

Câu 3: Huy thực hiện liên tiếp hai thí nghiệm. Thí nghiệm thứ nhất có xác suất thành công là 0,6. Nếu thí nghiệm thứ nhất thành công thì xác suất thành công của thí nghiệm thứ hai là 0,8. Nếu thí nghiệm thứ nhất không thành công thì xác suất thành công của thí nghiệm thứ hai là 0,3. Tính xác suất của biến cố: A: “Cả hai thí nghiệm đều thành công".

• A. 0,48

• B. 0,3
• C. 0,12
• D. 0,6

Câu 4: Nếu hai biến cố A, B thoả mãn P(B) = 0,4; P(A|B) = 0,5; P(A|) = 0,3 thì P(A) bằng:

• A. 0,38.

• B. 0,8.
• C. 0,2.
• D. 0,18.

Câu 5: Huy thực hiện liên tiếp hai thí nghiệm. Thí nghiệm thứ nhất có xác suất thành công là 0,6. Nếu thí nghiệm thứ nhất thành công thì xác suất thành công của thí nghiệm thứ hai là 0,8. Nếu thí nghiệm thứ nhất không thành công thì xác suất thành công của thí nghiệm thứ hai là 0,3. Tính xác suất của biến cố: B: “Thí nghiệm thứ nhất không thành công, còn thí nghiệm thứ hai thành công".

• A. 0,48
• B. 0,3

• C. 0,12

• D. 0,6

Câu 6: Nếu hai biến cố A, B thoả mãn P(A) = 0,3; P(B) = 0,6; P(A|B) = 0,4 thì P(B|A) bằng:

• A. 0,5.
• B. 0,6.

• C. 0,8.

• D. 0,2.

Câu 7: Có hai chiếc hộp, hộp I có 5 viên bi màu trắng và 5 viên bi màu đen, hộp II có 6 viên bi màu trắng và 4 viên bi màu đen, các viên bi có cùng kích thước và khối lượng. Tính xác suất để viên bi được lấy ra là viên bi màu trắng.

• A.
• B.
• C.

• D.

Câu 8: Có hai chiếc hộp, hộp I có 5 viên bi màu trắng và 5 viên bi màu đen, hộp II có 6 viên bi màu trắng và 4 viên bi màu đen, các viên bi có cùng kích thước và khối lượng. Giả sử viên bi được lấy ra là viên bi màu trắng. Tính xác suất viên bi màu trắng đó thuộc hộp I.

• A.
• B.
• C.

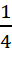
• D.

Câu 9: Cho hai biến cố A, B với P(B) = 0,6; P(A | B) = 0,7 và P(A | ) = 0,4. Khi đó, P(A) bằng:

• A. 0,7.
• B. 0,4.

• C. 0,58.

• D. 0,52.

Câu 10: Huy thực hiện liên tiếp hai thí nghiệm. Thí nghiệm thứ nhất có xác suất thành công là 0,6. Nếu thí nghiệm thứ nhất thành công thì xác suất thành công của thí nghiệm thứ hai là 0,8. Nếu thí nghiệm thứ nhất không thành công thì xác suất thành công của thí nghiệm thứ hai là 0,3. Tính xác suất của biến cố: C: “Thí nghiệm thứ hai thành công".

• A. 0,48
• B. 0,3
• C. 0,12

• D. 0,6

Câu 11: Một nhà máy sản xuất bóng đèn, máy A sản xuất 25%, máy B: 35%, máy C: 40% số bóng đèn. Tỉ lệ sản phẩm hỏng của mỗi máy trên số sản phẩm do máy đó sản xuất lần lượt là 3%, 2%, 1%. Một người mua 1 bóng đèn do nhà máy sản xuất. Tính xác suất để sản phẩm này tốt. 

• A. 0,9815

• B. 0,2162
• C. 0,8917
• D. 0,1275

Câu 12: Một lô hạt giống được phân thành ba loại. Loại 1 chiếm 2/3 số hạt cả lô, loại 2 chiếm 1/4, còn lại là loại 3. Loại 1 có tỉ lệ nẩy mầm 80%, loại 2 có tỉ lệ nẩy mầm 60% và loại 3 có tỉ lệ nẩy mầm 40%. Hỏi tỉ lệ nẩy mầm chung của lô hạt giống là bao nhiêu?

• A. 0,98
• B. 0,56
• C. 0,68

• D. 0,72

Câu 13: Hai nhà máy cùng sản xuất 1 loại linh kiện điện tử. Năng suất nhà máy hai gấp 3 lần năng suất nhà máy một. Tỷ lệ hỏng của nhà máy một và hai lần lượt là 0,1% và 0,2%. Giả sử linh kiện bán ở Trung tâm chỉ do hai nhà máy này sản xuất. Mua 1 linh kiện ở Trung tâm. Tính xác suất để linh kiện ấy hỏng.

• A. 0,175%

• B. 0,186%
• C. 0,179%
• D. 0,205%

Câu 14: Một chuồng gà có 9 con gà mái và 1 con gà trống. Chuồng gà kia có 1 con mái và 5 con trống. Từ mỗi chuồng lấy ngẫu nhiên 1 con đem bán. Các con gà còn lại được dồn vào chuồng thứ ba. Nếu ta lại bắt ngẫu nhiên 1 con gà nữa từ chuồng này ra thì xác suất để bắt được con gà trống là bao nhiêu?

• A. 0,5432
• B. 0,1296
• C. 0,1336

• D. 0,3619

Câu 15: Có 2 hộp áo; hộp một có 10 áo trong đó có 1 phế phẩm; hộp hai có 8 áo trong đó có 2 phế phẩm. Lấy ngẫu nhiên 1 áo từ hộp một bỏ sang hộp hai; sau đó từ hộp này chọn ngẫu nhiên ra 2 áo. Tìm xác suất để cả 2 áo này đều là phế phẩm. 

• A.

• B.
• C.
• D.

Câu 16: Có 3 xạ thủ cùng bắn vào một con thú, mỗi người bắn 1 viên đạn, với xác suất bắn trúng lần lượt là 0,6; 0,7; 0,8. Biết rằng nếu trúng 1 phát đạn thì xác suất để con thú bị tiêu diệt là 0,5; trúng 2 phát thì xác suất để con thú bị tiêu diệt là 0,8; còn nếu trúng 3 phát đạn thì chắc chắn con thú bị tiêu diệt. Tính xác suất con thú bị tiêu diệt.

• A. 0,7916

• B. 0,8764
• C. 0,9764
• D. 0,7534

Câu 17: Có 3 hộp bi; hộp một có 10 bi trong đó có 3 bi đỏ; hộp hai có 15 bi trong đó có 4 bi đỏ; hộp ba có 12 bi trong đó có 5 bi đỏ. Gieo một con xúc xắc. Nếu xuất hiện mặt 1 thì chọn hộp một, xuất hiện mặt hai thì chọn hộp 2, xuất hiện các mặt còn lại thì chọn hộp ba. Từ hộp được chọn, lấy ngẫu nhiên 1 bi. Giả sử lấy được bi đỏ. Tính xác suất để bi đỏ này thuộc hộp hai. 

• A. 0,1236

• B. 0,1194

• C. 0,2286
• D. 0,1243

Câu 18: Một hộp có 15 quả bóng bàn, trong đó có 9 mới 6 cũ, lần đầu chọn ra 3 quả để sử dụng, sau đó bỏ vào lại, lần hai chọn ra 3 quả. Tính xác suất 3 quả bóng chọn lần hai là 3 bóng mới.

• A. 0,5643
• B. 0,9864

• C. 0,0893

• D. 0,0432

Câu 19: Một hộp có 15 quả bóng bàn, trong đó có 9 mới 6 cũ, lần đầu chọn ra 3 quả để sử dụng, sau đó bỏ vào lại, lần hai chọn ra 3 quả. Biết rằng lần hai chọn được 3 bóng mới, tính xác suất lần đầu chọn được 2 bóng mới.

• A. 0,9863
• B. 0,4532
• C. 0,3495

• D. 0,4089

Câu 20: Có 3 cái thùng. Thùng 1 có 6 bi trắng, 4 bi đỏ; thùng 2 có 5 bi trắng, 5 bi đỏ và thùng 3 có 10 bi trắng. Giả sử người ta lấy ngẫu nhiên 2 bi từ thùng 1 bỏ vào thùng 2. Sau đó, lại lấy ngẫu nhiên 1 bi từ thùng 2 bỏ vào thùng 3 rồi từ thùng 3 lấy ngẫu nhiên ra 1 bi. Tìm xác suất để bi lấy ra là đỏ.

• A. 0,0234
• B. 0,8345
• C. 0,0546

• D. 0,0439