Siêu nhanh giải bài 2 chương VI toán 12 Cánh diều tập 2
Giải siêu nhanh bài 2 chương VI toán 12 Cánh diều tập 2. Giải siêu nhanh toán 12 Cánh diều tập 2. Những phần nào có thể rút gọn, lược bỏ và tóm gọn. Đều được áp dụng vào bài giải này. Thêm cách giải mới để học sinh lựa chọn. Để tìm ra phong cách học toán 12 Cánh diều tập 2 phù hợp với mình.
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
BÀI 2. CÔNG THỨC XÁC SUẤT TOÀN PHẦN. CÔNG THỨC BAYES
I. CÔNG THỨC XÁC SUẤT TOÀN PHẦN
Hoạt động 1:
Một hộp có 24 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, ..., 24; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên 1 chiếc thẻ trong hộp. Xét các biến cố A: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 3” và biến cố B: “Số xuất hiện trên thẻ được rút ra là số chia hết cho 4”.
a) Viết các tập con của không gian mẫu tương ứng với các biến cố ![]()
b) So sánh:
![]()
Từ đó, hãy chứng tỏ rằng:
![]()
c) So sánh:
![]()
![]()
Từ đó, hãy chứng tỏ rằng:
![]()
Giải rút gọn:
a) Không gian mẫu S:
![]()
Biến cố A: "Số xuất hiện trên thẻ được rút ra là số chia hết cho 3"
![]()
![]()
Biến cố B: "Số xuất hiện trên thẻ được rút ra là số chia hết cho 4"
![]()
![]()
Biến cố A∩B: "Số xuất hiện trên thẻ được rút ra là số chia hết cho 3 và 4" (chia hết cho 12)
![]()
![]()
Biến cố A∩B̅: "Số xuất hiện trên thẻ được rút ra là số chia hết cho 3 nhưng không chia hết cho 4"
![]()
![]()
b) ![]()
![]()
![]()
Vậy ![]()
Ta có:
![]()
![]()
![]()
![]()
Vậy ![]()
c) ![]()
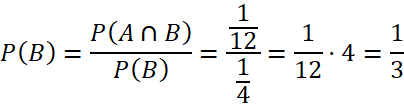
![]()
Vậy ![]()
So sánh ![]() và
và ![]()
![]()

![]()
Vậy ![]()
Ta có:
![]()
Vậy:
![]()
Luyện tập - vận dụng 1:
Hãy giải bài toán trong phần mở đầu bằng cách lập bảng thống kê như trong Ví dụ 2, biết rằng cả hai nhà máy sản xuất được 10 000 linh kiện.
Giải rút gọn:
Số linh kiện ở nhà máy 1:
![]()
Số linh kiện đạt tiêu chuẩn ở nhà máy 1:
![]()
Số linh kiện không đạt tiêu chuẩn ở nhà máy I:
![]()
Số linh kiện ở nhà máy 2:
![]()
Số linh kiện đạt tiêu chuẩn ở nhà máy 2:
![]()
Số linh kiện không đạt tiêu chuẩn ở nhà máy 2:
![]()
Ta có bảng sau:
| Linh kiện đạt tiêu chuẩn | Linh kiện không đạt tiêu chuẩn | |
| Nhà máy 1 | 4950 | 550 |
| Nhà máy 2 | 3985 | 585 |
Xét các biến cố sau:
A: biến cố linh kiện được lấy ra là sản phẩm của nhà máy I.
A’: biến cố linh kiện được lấy ra là sản phẩm của nhà máy II.
B: biến cố linh kiện được lấy ra đạt tiêu chuẩn.
P(A) = ![]()
P(B/A) = ![]()
P(B/A’) = ![]()
Xác suất để linh kiện được lấy ra đạt tiêu chuẩn là:
![]()
Vậy, xác suất để linh kiện được lấy ra đạt tiêu chuẩn là 0,8925 hoặc 89,25%
Luyện tập - vận dụng 2:
Luyện tập 2: Hãy giải bài toán trong phần mở đầu bằng phương pháp sử dụng sơ đồ hình cây như trong ví dụ 3:
Giải rút gọn:
Xét các biến cố
A: biến cố linh kiện được lấy ra là sản phẩm của nhà máy I.
B: biến cố linh kiện được lấy ra là sản phẩm của nhà máy II
C: biến cố linh kiện được lấy ra đạt tiêu chuẩn.
D: biến cố linh kiện được lấy ra không đạt tiêu chuẩn.
Sơ đồ hình cây biểu diễn bài toán:
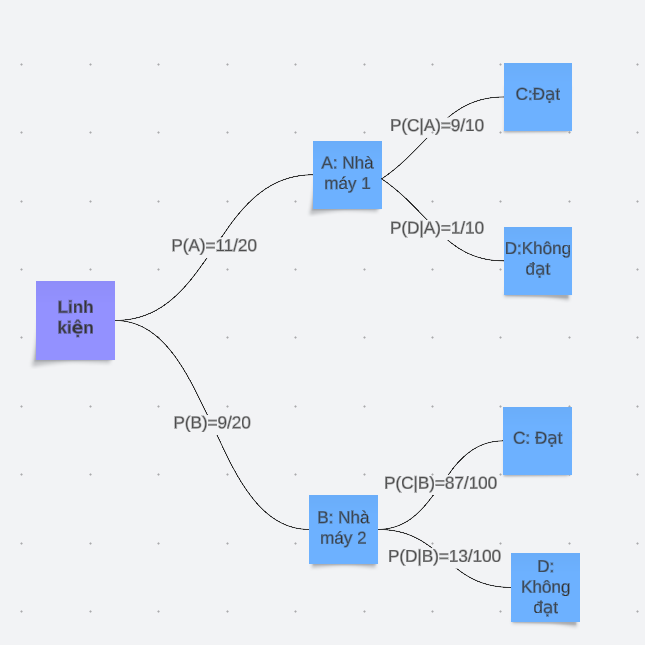
Xác suất để linh kiện được lấy ra đạt tiêu chuẩn là:
![]()
II. CÔNG THỨC BAYES
Hoạt động 2:
Xét hai biến cố A, B trong Hoạt động 1.
a) Tính: P(A), P(B), ![]() và P(B|A).
và P(B|A).
b) So sánh: P(B|A) và ![]()
Giải rút gọn:
Không gian mẫu S:
![]()
Biến cố A: "Số xuất hiện trên thẻ được rút ra là số chia hết cho 3"
![]()
![]()
Biến cố B: "Số xuất hiện trên thẻ được rút ra là số chia hết cho 4"
![]()
![]()
a) Ta có:
![]()
![]()
Biến cố A ∩ B: "Số xuất hiện trên thẻ được rút ra là số chia hết cho cả 3 và 4" (chia hết cho 12):
![]()
Ta có:
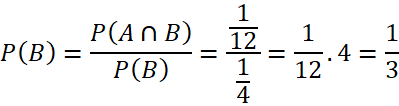

b) ![]()
Vậy P(B|A) = ![]()
Luyện tập - vận dụng 3:
Cho hai biến cố A, B sao cho P(A) = 0,4, P(B) = 0,8, P(B|A) = 0,3
Tính P(A|B).
Giải rút gọn:
Sử dụng công thức Bayes:
![]()
Luyện tập - vận dụng 4:
Được biết có 5% đàn ông bị mù màu, và 0,25% phụ nữ bị mù màu (Nguồn: F. M. Dekking et al., A modern introduction to probability and statistics - Understanding why and how, Springer, 2005). Giả sử số đàn ông bằng số phụ nữ. Chọn một người bị mù màu một cách ngẫu nhiên. Hỏi xác suất để người đó là đàn ông là bao nhiêu?
Giải rút gọn:
Xét các biến cố:
- D: Chọn ngẫu nhiên một người bị mù màu.
- M: Người đó là đàn ông.
- W: Người đó là phụ nữ.
- Xác suất để một người đàn ông bị mù màu: ![]()
- Xác suất để một người phụ nữ bị mù màu: ![]() .
.
- Giả sử số đàn ông bằng số phụ nữ: ![]() .
.
Tính xác suất để một người ngẫu nhiên bị mù màu ![]()
![]()
![]()
![]()
![]()
Xác suất để 1 người đàn ông bị mù màu:
![]()
![]()
![]()
![]()
Xác suất để một người ngẫu nhiên bị mù màu là đàn ông là khoảng ![]() 0.9524 hay 95,24%
0.9524 hay 95,24%
GIẢI BÀI TẬP CUỐI SÁCH GIÁO KHOA
Bài 1:
Cho hai biến cố A, B với P(B) = 0,6; P(A | B) = 0,7 và ![]() . Khi đó, P(A) bằng:
. Khi đó, P(A) bằng:
A. 0,7.
B. 0,4.
C. 0,58.
D. 0,52.
Giải rút gọn:
Tính ![]()
![]()
Tính ![]()
![]()
Bây giờ, ta tính P(A):
![]()
Vậy, P(A) bằng 0,58. Đáp án đúng là:C. 0,58.
Bài 2:
Có hai chiếc hộp, hộp I có 5 viên bi màu trắng và 5 viên bi màu đen, hộp II có 6 viên bi màu trắng và 4 viên bi màu đen, các viên bi có cùng kích thước và khối lượng.
a) Tính xác suất để viên bi được lấy ra là viên bi màu trắng.
b) Giả sử viên bi được lấy ra là viên bi màu trắng. Tính xác suất viên bi màu trắng đó thuộc hộp I.
Giải rút gọn:
Xét các biến cố:
- ![]() biến cố chọn hộp I.
biến cố chọn hộp I.
- ![]() : biến cố chọn hộp II.
: biến cố chọn hộp II.
- B :biến cố chọn được viên bi màu trắng.
Ta có:
- ![]()
- Xác suất lấy được viên bi màu trắng từ hộp I:
![]()
- Xác suất lấy được viên bi màu trắng từ hộp II:
![]()
Sử dụng công thức xác suất toàn phần:
![]()
![]()
![]()
![]()
Vậy, xác suất để viên bi được lấy ra là viên bi màu trắng là ![]() .
.
b)Giả sử viên bi được lấy ra là viên bi màu trắng, xác suất viên bi màu trắng đó thuộc hộp I là ![]()
Sử dụng định lý Bayes ta có:
![]()

Vậy, xác suất để viên bi màu trắng đó thuộc hộp I là ![]() .
.
Bài 3:
Một loại linh kiện do hai nhà máy số I, số II cùng sản xuất. Tỉ lệ phế phẩm của các nhà máy I, II lần lượt là: 4%; 3%. Trong một lô linh kiện để lẫn lộn 80 sản phẩm của nhà máy số 1 và 120 sản phẩm của nhà máy số II. Một khách hàng lấy ngẫu nhiên một linh kiện từ lô hàng đó.
a) Tính xác suất để linh kiện được lấy ra là linh kiện tốt.
b) Giả sử linh kiện được lấy ra là linh kiện phế phẩm. Xác suất linh kiện đó do nhà máy nào sản xuất là cao nhất?
Giải rút gọn:
- ![]() biến cố lấy sản phẩm từ nhà máy I
biến cố lấy sản phẩm từ nhà máy I
- ![]() biến cố lấy sản phẩm từ nhà máy II
biến cố lấy sản phẩm từ nhà máy II
- ![]() : biến cố sản phẩm lấy ra là sản phẩm tốt
: biến cố sản phẩm lấy ra là sản phẩm tốt
Xác suất chọn sản phẩm từ mỗi nhà máy:
![]()
![]()
Tỉ lệ phế phẩm:
- Nhà máy I: 4% tức ![]()
- Nhà máy II: 3% tức ![]()
Tỉ lệ sản phẩm tốt:
![]()
![]()
Sử dụng công thức xác suất toàn phần:
![]()
![]()
![]()
![]()
Vậy, xác suất để linh kiện được lấy ra là linh kiện tốt là 0.966 hay 96.6%.
b) Xét biến cố
- ![]() biến cố sản phẩm lấy ra là phế phẩm
biến cố sản phẩm lấy ra là phế phẩm
Sử dụng định lý Bayes:
Xác suất lấy phế phẩm từ nhà máy 1:
![]()
Xác suất lấy phế phẩm từ nhà máy 2:
![]()
Mà ![]()
Vậy ![]()
![]()
![]()
Vậy, xác suất để linh kiện phế phẩm thuộc nhà máy II là cao nhất.
Bài 4:
Năm 2001, Cộng đồng châu Âu có làm một đợt kiểm tra rất rộng rãi các con bò để phát hiện những con bị bệnh bò điên. Không có xét nghiệm nào cho kết quả chính xác 100%. Một loại xét nghiệm, mà ở đây ta gọi là xét nghiệm A, cho kết quả như sau: khi con bò bị bệnh bò điên thì xác suất để có phản ứng dương tính trong xét nghiệm A là 70%, còn khi con bò không bị bệnh thì xác suất để có phản ứng dương tính trong xét nghiệm A là 10%. Biết rằng tỉ lệ bò bị mắc bệnh bò điên ở Hà Lan là 13 con trên 1 000 000 con (Nguồn: F. M. Dekking et al., A modern introduction to probability and statistics-Understanding why and how, Springer, 2005). Hỏi khi một con bò ở Hà Lan có phản ứng dương tính với xét nghiệm A thì xác suất để nó bị mắc bệnh bò điên là bao nhiêu?
Giải rút gọn:
Xét các biến cố:
-B: biến cố một con bò bị bệnh bò điên
-![]() : biến cố 1 con bò không bị bệnh bò điên
: biến cố 1 con bò không bị bệnh bò điên
- T: biến cố 1 con bò phản ứng dương tính.
- Xác suất một con bò bị bệnh bò điên: ![]()
- Xác suất một con bò không bị bệnh bò điên: ![]()
- Xác suất xét nghiệm cho kết quả dương tính nếu bò bị bệnh: ![]()
- Xác suất xét nghiệm cho kết quả dương tính nếu bò không bị bệnh:![]()
Xác suất để một con bò bị bệnh bò điên khi xét nghiệm cho kết quả dương tính, tức là ![]()
Sử dụng định lý Bayes:
![]()
Trong đó:
![]()
![]()
Tính ![]()
![]()
Xác suất để một con bò ở Hà Lan bị mắc bệnh bò điên khi xét nghiệm A cho kết quả dương tính là khoảng 0.000091, hay 0.0091%.
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
Nội dung quan tâm khác
Thêm kiến thức môn học
Giải toán 12 Cánh diều tập 2 bài 2 chương VI, Giải bài 2 chương VI toán 12 Cánh diều tập 2, Siêu nhanh giải bài 2 chương VI toán 12 Cánh diều tập 2
Giải bài tập những môn khác
Môn học lớp 12 KNTT
5 phút giải toán 12 KNTT
5 phút soạn bài văn 12 KNTT
Văn mẫu 12 KNTT
5 phút giải vật lí 12 KNTT
5 phút giải hoá học 12 KNTT
5 phút giải sinh học 12 KNTT
5 phút giải KTPL 12 KNTT
5 phút giải lịch sử 12 KNTT
5 phút giải địa lí 12 KNTT
5 phút giải CN lâm nghiệp 12 KNTT
5 phút giải CN điện - điện tử 12 KNTT
5 phút giải THUD12 KNTT
5 phút giải KHMT12 KNTT
5 phút giải HĐTN 12 KNTT
5 phút giải ANQP 12 KNTT
Môn học lớp 12 CTST
5 phút giải toán 12 CTST
5 phút soạn bài văn 12 CTST
Văn mẫu 12 CTST
5 phút giải vật lí 12 CTST
5 phút giải hoá học 12 CTST
5 phút giải sinh học 12 CTST
5 phút giải KTPL 12 CTST
5 phút giải lịch sử 12 CTST
5 phút giải địa lí 12 CTST
5 phút giải THUD 12 CTST
5 phút giải KHMT 12 CTST
5 phút giải HĐTN 12 bản 1 CTST
5 phút giải HĐTN 12 bản 2 CTST
Môn học lớp 12 cánh diều
5 phút giải toán 12 CD
5 phút soạn bài văn 12 CD
Văn mẫu 12 CD
5 phút giải vật lí 12 CD
5 phút giải hoá học 12 CD
5 phút giải sinh học 12 CD
5 phút giải KTPL 12 CD
5 phút giải lịch sử 12 CD
5 phút giải địa lí 12 CD
5 phút giải CN lâm nghiệp 12 CD
5 phút giải CN điện - điện tử 12 CD
5 phút giải THUD 12 CD
5 phút giải KHMT 12 CD
5 phút giải HĐTN 12 CD
5 phút giải ANQP 12 CD
Giải chuyên đề học tập lớp 12 kết nối tri thức
Giải chuyên đề Ngữ văn 12 Kết nối tri thức
Giải chuyên đề Toán 12 Kết nối tri thức
Giải chuyên đề Vật lí 12 Kết nối tri thức
Giải chuyên đề Hóa học 12 Kết nối tri thức
Giải chuyên đề Sinh học 12 Kết nối tri thức
Giải chuyên đề Kinh tế pháp luật 12 Kết nối tri thức
Giải chuyên đề Lịch sử 12 Kết nối tri thức
Giải chuyên đề Địa lí 12 Kết nối tri thức
Giải chuyên đề Tin học ứng dụng 12 Kết nối tri thức
Giải chuyên đề Khoa học máy tính 12 Kết nối tri thức
Giải chuyên đề Công nghệ 12 Điện - điện tử Kết nối tri thức
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Kết nối tri thức
Giải chuyên đề học tập lớp 12 chân trời sáng tạo
Giải chuyên đề Ngữ văn 12 Chân trời sáng tạo
Giải chuyên đề Toán 12 Chân trời sáng tạo
Giải chuyên đề Vật lí 12 Chân trời sáng tạo
Giải chuyên đề Hóa học 12 Chân trời sáng tạo
Giải chuyên đề Sinh học 12 Chân trời sáng tạo
Giải chuyên đề Kinh tế pháp luật 12 Chân trời sáng tạo
Giải chuyên đề Lịch sử 12 Chân trời sáng tạo
Giải chuyên đề Địa lí 12 Chân trời sáng tạo
Giải chuyên đề Tin học ứng dụng 12 Chân trời sáng tạo
Giải chuyên đề Khoa học máy tính 12 Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Điện - điện tử Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Chân trời sáng tạo
Giải chuyên đề học tập lớp 12 cánh diều
Giải chuyên đề Ngữ văn 12 Cánh diều
Giải chuyên đề Toán 12 Cánh diều
Giải chuyên đề Vật lí 12 Cánh diều
Giải chuyên đề Hóa học 12 Cánh diều
Giải chuyên đề Sinh học 12 Cánh diều
Giải chuyên đề Kinh tế pháp luật 12 Cánh diều
Giải chuyên đề Lịch sử 12 Cánh diều
Giải chuyên đề Địa lí 12 Cánh diều
Giải chuyên đề Tin học ứng dụng 12 Cánh diều
Giải chuyên đề Khoa học máy tính 12 Cánh diều
Giải chuyên đề Công nghệ 12 Điện - điện tử Cánh diều
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Cánh diều

Bình luận