BÀI 2. NGUYÊN HÀM CỦA MỘT SỐ HÀM SỐ SƠ CẤP

I. NGUYÊN HÀM CỦA HÀM SỐ LŨY THỪA

Hoạt động 1:

Hàm số có là nguyên hàm của hàm số hay không?

Giải rút gọn:

Hàm số là nguyên hàm của hàm số vì

Luyện tập - vận dụng 1:

Tìm:

Giải rút gọn:

Luyện tập - vận dụng 2:

Tìm:

a)  

b)

Giải rút gọn:

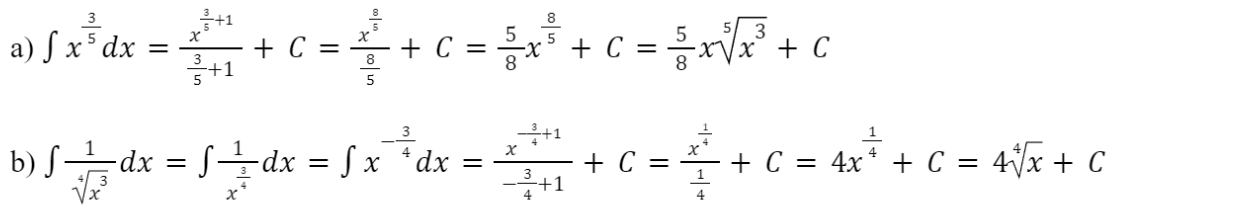
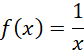
II. NGUYÊN HÀM CỦA HÀM SỐ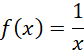

Hoạt động 2:

a) Tính đạo hàm của hàm số trên khoảng (0;+∞)

b) Tính đạo hàm của hàm số trên khoảng (0;+∞)

Giải rút gọn:

a)  trên khoảng (0;+∞)

b) trên khoảng (-∞;0)

Luyện tập - vận dụng 3:

Tìm

Giải rút gọn:

III. NGUYÊN HÀM CỦA HÀM SỐ LƯỢNG GIÁC 

Hoạt động 3:

a) Hàm số có là nguyên hàm của hàm số hay không?

b) Hàm số có là nguyên hàm của hàm số hay không?

c) Với , , hàm số có là nguyên hàm của hàm số  hay không?

d) Với , , hàm số có là nguyên hàm của hàm số  hay không?

Giải rút gọn:

a) Hàm số là nguyên hàm của hàm số vì

b) Hàm số là nguyên hàm của hàm số vì

c) Ta có:

Tính đạo hàm của :

Do đó hàm số là nguyên hàm của hàm số  với ,

d) Ta có:

Với , , hàm số là nguyên hàm của hàm số  .

Luyện tập - vận dụng 4:

Tìm:

a)

b)

Giải rút gọn:

Luyện tập - vận dụng 5:

Tìm:

a)

b)

Giải rút gọn:

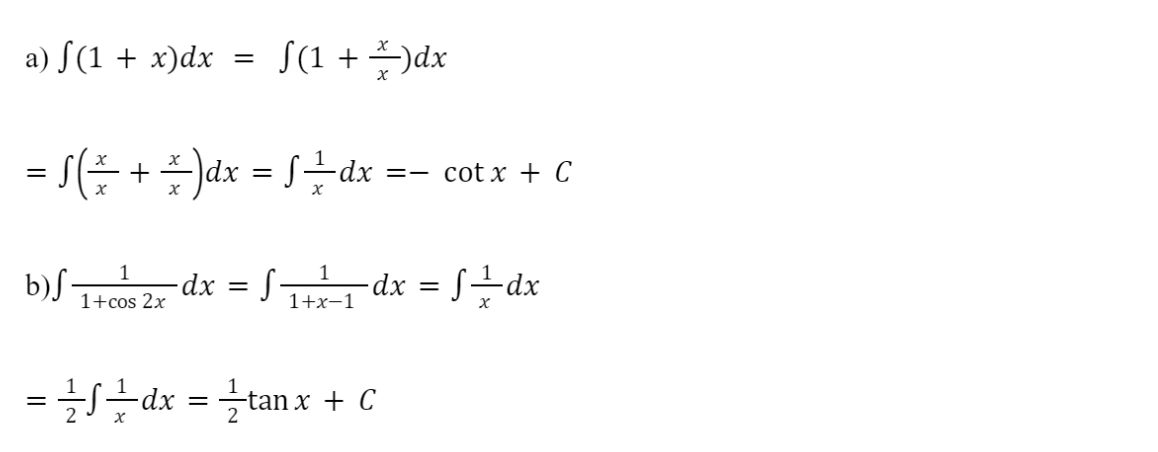
IV. NGUYÊN HÀM CỦA HÀM SỐ MŨ 

Hoạt động 4:

Tính đạo hàm của hàm số Từ đó nêu một nguyên hàm của hàm số

Giải rút gọn:

Ta có:

Đạo hàm của hàm số là . Vì vậy là một nguyên hàm của .

Luyện tập - vận dụng 6:

Tìm: 

a)

b)

Giải rút gọn :

GIẢI BÀI TẬP CUỐI SÁCH GIÁO KHOA

Bài 1:

bằng:

A.

B.

C.

D.

Giải rút gọn: 

Đáp án D

Bài 2:

bằng:

A.

B.

C.

D.

Giải rút gọn:

Đáp án C.

Bài 3:

Nguyên hàm của hàm số bằng:

A.

B.

C.

D.

Giải rút gọn:

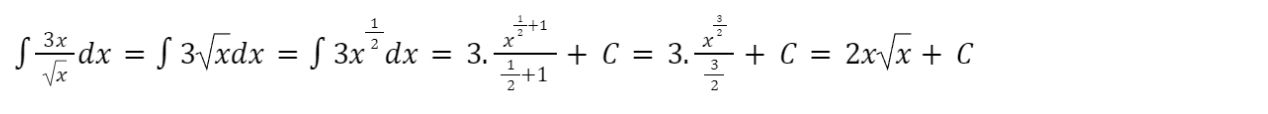
Đáp án D.

Bài 4:

Nguyên hàm của hàm số bằng:

A.

B.

C.

D.

Giải rút gọn : 

Đáp án B. 

Bài 5:

Tìm:

a)

b)

c)

d)

Giải rút gọn: 

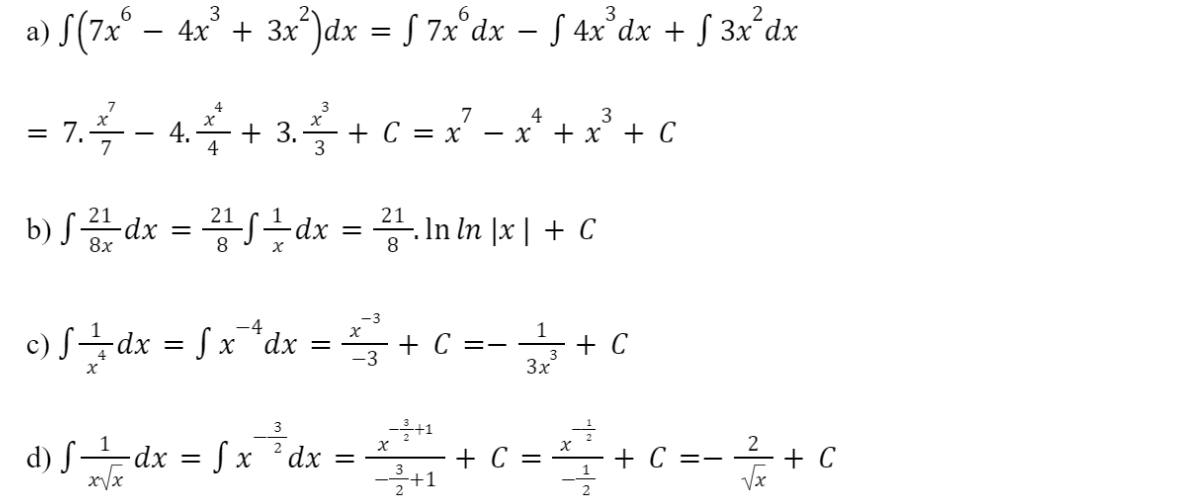
Bài 6: 

Tìm:

a.

b.

c.

d.

Giải rút gọn:

Bài 7:

Cây cà chua khi trồng có chiều cao 5 cm. Tốc độ tăng chiều cao của cây cà chua sau khi trồng được cho bởi hàm số

Trong đó t tính theo tuần, v(t) tính theo centimet/tuần. Gọi h(t) (tính bằng centimet) là độ cao của cây cà chua ở tuần thứ t. (Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma-I, Cornelsen 2016).

a) Viết công thức xác định hàm số h(t) (t ≥ 0).

b) Giai đoạn tăng trưởng của cây cà chua đó kéo dài bao lâu?

c) Chiều cao tối đa của cây là bao nhiêu centimet?

d) Vào thời điểm cây cà chua đó phát triển nhanh nhất thì cây cà chua đó cao bao nhiêu centimet?

Giải rút gọn:

a) Để xác định hàm số h(t), ta tính nguyên hàm của hàm v(t):

Mà cây cà chua khi mới trồng có chiều cao 5cm. Thay t = 0 vào h(t):

Vậy C=5. Hàm số h(t) (t ≥ 0):

b) Giai đoạn tăng trưởng của cây cà chua kéo dài cho đến khi tốc độ tăng trưởng v(t) bằng 0. Ta có:

Phương trình có nghiệm t=0 và t=10. Vì vậy, giai đoạn tăng trưởng kéo dài từ tuần 1 đến tuần thứ 10. 

c) Chiều cao tối đa của cây cà chua có được khi nó ở tuần cuối của giai đoạn tăng trưởng. Vì giai đoạn tăng trưởng kéo dài đến tuần thứ 10, vì vậy chiều cao tối đa của cây sẽ đạt được khi t=10:

Vậy chiều cao tối đa của cây cà chua là 88,33cm.

d) Để tìm thời điểm cây cà chua phát triển nhanh nhất, ta cần tính giá trị của t mà tại t, v(t) đạt giá trị cực đại. Ta có

Ta có: khi . Thay giá trị t vào biểu thức

Vậy tại tuần thứ cây cà chua có tốc độ tăng trưởng lớn nhất.

Bài 8:

Một quần thể vi khuẩn ban đầu gồm 500 vi khuẩn, sau đó bắt đầu tăng trưởng. Gọi P(t) là số lượng vi khuẩn của quần thể đó tại thời điểm t, trong đó t tính theo ngày (0 ≤ t ≤ 10). Tốc độ tăng trưởng của quần thể vi khuẩn đó được cho bởi hàm số trong đó k là hằng số. Sau 1 ngày, số lượng quần thể của vi khuẩn đó đã tăng lên thành 600 vi khuẩn. ( (Nguồn R.Larson and B. Edwards, Calculus 10e Cengage 2014). Tính số lượng vi khuẩn của quần thể đó sau 7 ngày (làm tròn kết quả đến hàng đơn vị).

Giải rút gọn:

Số lượng vi khuẩn tăng trưởng sẽ được tính bởi hàm P(t), với P(t) là nguyên hàm của hàm P’(t):

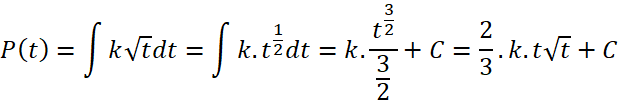
Điều kiện ban đầu P(0)=500:

C=500

Sau 1 ngày, số lượng vi khuẩn tăng thành 600:

Ta có hàm P(t):

Sau 7 ngày, số lượng vi khuẩn là:

Vậy số lượng vi khuẩn sau 7 ngày là 2352 vi khuẩn.