BÀI TẬP CUỐI CHƯƠNG IV

Bài 1:

Cho hàm số Nguyên hàm F(x) cảu hàm số f(x) trên R sao cho F(0) bằng 2023 là:

A.

B.

C.

D.

Giải rút gọn:

Mà:

Nguyên hàm F(x):

Đáp án C.

Bài 2:

Biết  là một nguyên hàm của hàm f(x) trên R. Giá trị của bẳng:

A.

B. 7

C. 9

D.

Giải rút gọn:

Đáp án C.

Bài 3:

Biết Khi đó  bằng

A.1

B. 4

C. 2

D. 0

Giải rút gọn:

Vậy

Đáp án A.

Bài 4:

Tìm:

a)

b)

c)

d)

e)

g)

Giải rút gọn:

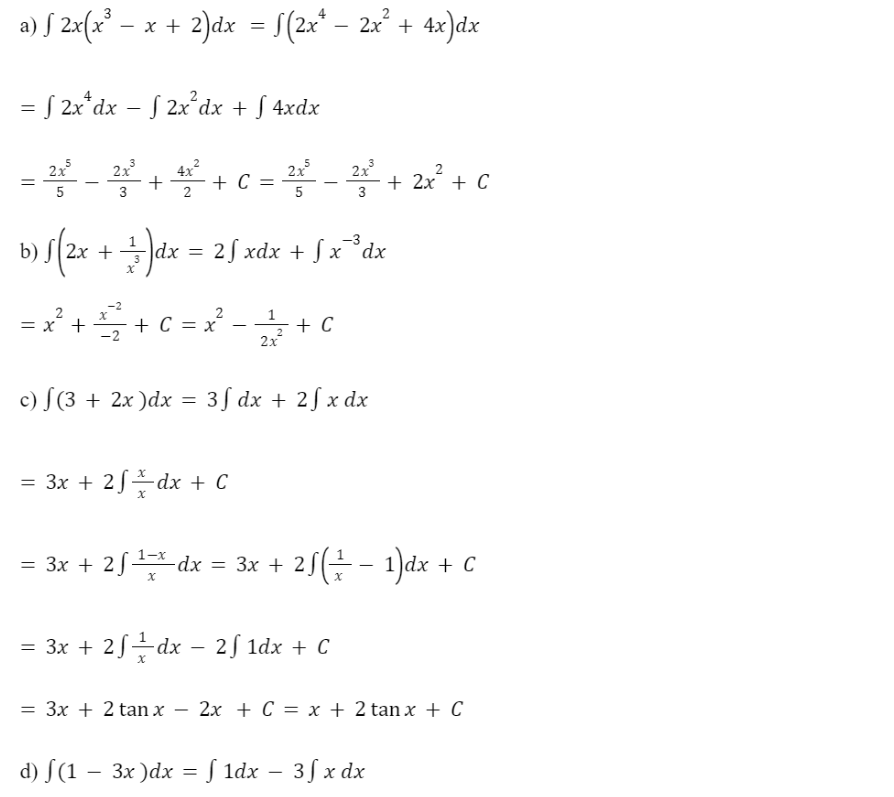
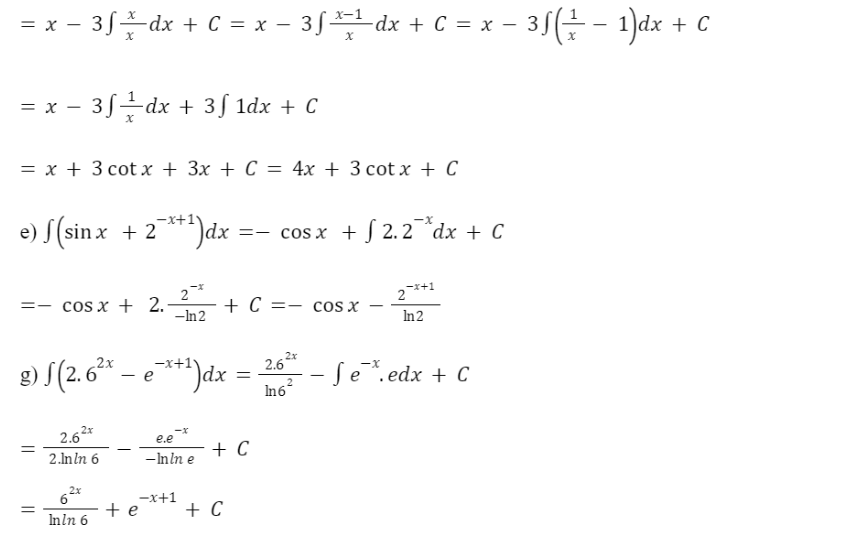
Bài 5:

a) Tìm nguyên hàm F(x) của hàm số trên R sao cho F(0) = 2023.

b) Tìm nguyên hàm G(x) của hàm số trên khoảng (0; +∞) sao cho G(1) = 2023.

Giải rút gọn:

Mà F(0)=2023

b)

Mà G(1)= 2023 

Bài 6:

a)

b)

c)

d)

e)

g)

Giải rút gọn:

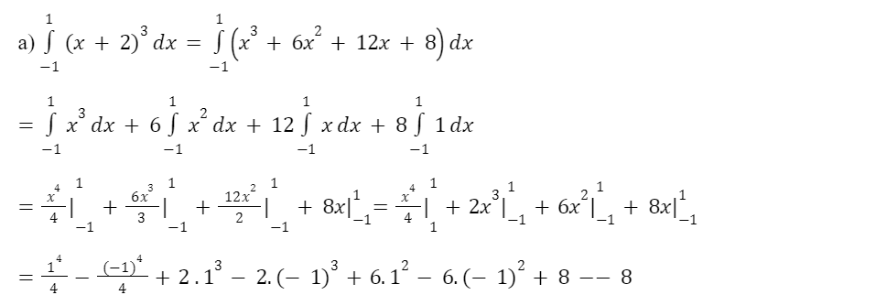
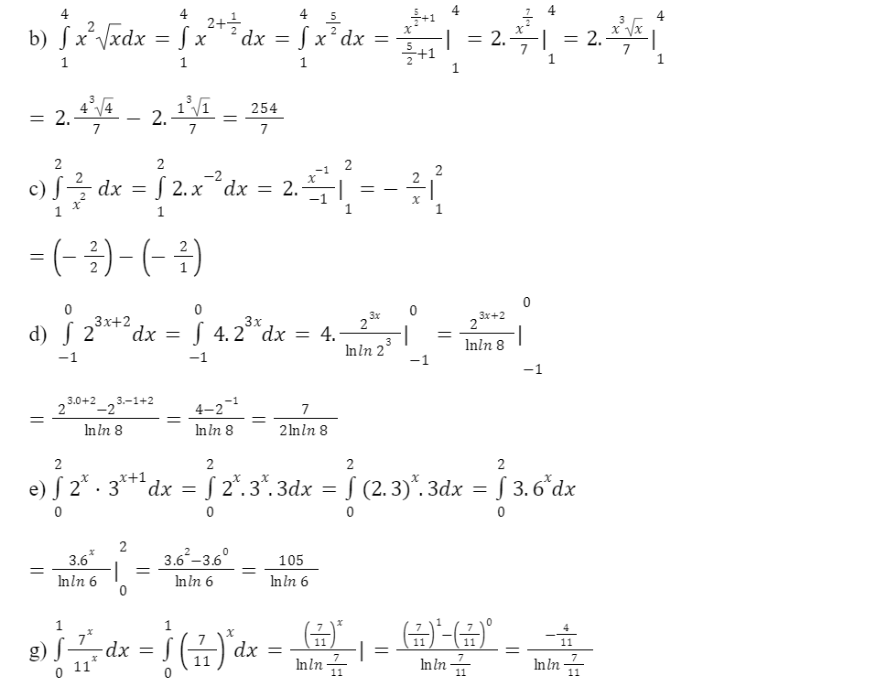
Bài 7:

Một khinh khí cầu bay với độ cao (so với mực nước biển) tại thời điểm t là h(t), trong đó 1 tính bằng phút, h(1) tính bằng mét. Tốc độ bay của khinh khí cầu được cho bởi hàm số

Với t tính bằng phút, v(t) tính bằng mét/phút. Tại thời điểm xuất phát (t=0) khinh khí cầu ở độ cao 520 m và 5 phút sau khi xuất phát, khinh khí cầu đã ở độ cao 530 m.

a) Viết công thức xác định hàm số biểu thị độ cao của khinh khí cầu tại thời điểm (t).

b) Độ cao tối đa của khinh khí cầu khi bay là bao nhiêu?

c) Khi nào khinh khí cầu sẽ trở lại độ cao khi xuất phát?

Giải rút gọn:

a) Hàm độ cao h(t) là một nguyên hàm của hàm v(t)

Ta có tại thời điểm xuất phát (t=0) khinh khí cầu ở độ cao 520 m, vậy h(0)=520:

Do đó hàm h(t) là:

Tại t=5, ta có:

h(5) bằng 130, thỏa mãn điều kiện đề bài. Vậy ta có hàm h(t):

b) Để tìm độ cao tối đa, chúng ta tìm đạo hàm h’(t) và tìm điểm làm cho h’(t)=0:

h’(t)=0:

t =0 hoặc t = 10

Ta kiểm tra giá trị h tại t=10:

Vậy độ cao tối đa là 540 mét.

c) Để tìm thời điểm khinh khí cầu trở lại độ cao xuất phát, ta cần tìm t khi h(t)=520:

t = 0 hoặc t=15. Mà t=0 là thời điểm xuất phát. Vậy khinh khí cầu sẽ trở lại độ cao ban đầu sau 15 phút.

Bài 8: 

Một công trình xây dựng dự kiến hoàn thành trong 100 ngày. Số lượng công nhân được sử dụng tại thời điểm t cho bởi hàm số:

trong đó t tính theo ngày (0≤ t ≤100), m(t) tính theo người.

(Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma-1, Cornelsen 2016)

a) Khi nào có 360 công nhân được sử dụng?

b) Khi nào số công nhân được sử dụng lớn nhất?

c) Gọi M(t) là số ngày công được tính đến hết ngày thứ t (kể từ khi khởi công công trình). Trong kinh tế xây dựng, người ta đã biết rằng M'(t) = m(t). Tổng cộng cần bao nhiêu ngày công để hoàn thành công trình xây dựng đó?

Giải rút gọn

a) Số công nhân được sử dụng là 360:

Ta giải phương trình m(t) = 360:

Đặt ta có , phương trình trở thành:

Giải phương trình bậc hai:

Vì  và ta chỉ lấy nghiệm u=7:

Vậy, có 360 công nhân được sử dụng vào thời điểm 49 ngày.

b) Khi nào số công nhân được sử dụng lớn nhất?

Để tìm số công nhân được sử dụng lớn nhất, ta cần tìm giá trị cực đại của hàm m(t):

Tính đạo hàm của m(t):

Đặt m’(t)=0:

Tính m’’(t):

Vậy t là điểm cực đại, số công nhân được sử dụng lớn nhất là

Vậy, số công nhân lớn nhất là 562 người tại

c) Số ngày công cần thiết để hoàn thành là:

Vậy, tổng số ngày công cần để hoàn thành công trình là 33333 ngày.

Bài 9:

Trong bài này, ta xét một tình huống giả định có một học sinh sau kì nghỉ đã mang virus cúm quay trở lại khuôn viên trường học biệt lập. Sau khi có sự tiếp xúc giữa các học sinh, virus cúm lây lan trong khuôn viên trường. Giả thiết hệ thống chống dịch chưa được khởi động và virus cúm được lây lan tự nhiên. Gọi P(t) là số học sinh bị nhiễm virus cúm ở ngày thứ t tính từ ngày học sinh mang virus cúm quay trở lại khuôn viên trường. Biết rằng tốc độ lây lan của virus cúm cho bởi công thức trong đó C là hằng số khác 0. Số học sinh bị nhiễm virus cúm sau 4 ngày là 55 học sinh. Xác định số học sinh bị nhiễm virus cúm sau 10 ngày.

Giải rút gọn:

Để xác định số học sinh bị nhiễm virus cúm sau 10 ngày, ta cần tìm ra phương trình hàm P(t):

Ta có số học sinh bị nhiễm virus ở ngày thứ 0 là 0:

Số học sinh bị nhiễm ngày thứ 4 là 55:

Hàm P(t):

Số học sinh bị nhiễm virus cúm sau 10 ngày:

Vậy số học sinh bị nhiễm virus cúm sau 10 ngày là 130 học sinh.

Bài 10:

Một chiếc xe ô tô chạy thử nghiệm trên một đường thẳng bắt đầu từ trạng thái đứng yên. Tốc độ của chiếc xe ô tô đó (tính bằng mét/giây) lần lượt ở giây thứ 10, thứ 20, thứ 30, thứ 40, thứ 50 và thứ 60 được ghi lại trong Bảng 1:

a) Xây dựng hàm số bậc ba để biểu diễn các số liệu ở Bảng 1, tức là ở hệ trục tọa độ Oxy, đồ thị của hàm số đó trên nửa khoảng [0; +∞) “gần” với các điểm 0(0; 0), B(10; 5), C(20; 21), D(30; 40), E(40; 62), G(50; 78), K(60; 83) (Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014).

b) Tính (gần đúng) quãng đường mà xe ô tô đó đã đi được tính đến giây thứ 60 của quá trình thử nghiệm.

Giải rút gọn:

a) Xây dựng hàm số bậc ba  

Từ các điểm dữ liệu trong Bảng 1, ta có hệ phương trình sau:

Hay:

Giải hệ các phương trình, ta có  hàm f(x):

b) Quãng đường mà xe ô tô đã đi được tính đến giây thứ 60 là tích phân của hàm số vận tốc v(t) = f'(t) từ t = 0 đến t = 60.

Quãng đường mà xe ô tô đã đi được tính đến giây thứ 60 là 2473 mét.

Bài 11:

Giả sử A, B lần lượt là diện tích các hình được tô màu ở Hình 37 

a) Tính các diện tích A, B

 b) Biết B = 3A. Biểu diễn b theo a

Giải rút gọn:

a) Diện tích A, B được tính như sau:             

Hình phẳng A được giới hạn bởi trục hoành Ox, các đường

Hình phẳng B được giới hạn bởi trục hoành Ox, các đường

b) Ta có B=3A

Bài 12: 

Hình 38 minh họa mặt cắt đứng của một bức tường cũ có dạng hình chữ nhật với một cổng ra vào có dạng hình parabol với các kích thước được cho như trong hình đó. Người ta dự định sơn lại mặt ngoài của bức tường đó. Chi phí để sơn bức tường là 15.000 đồng/1 m². Tổng chi phí để sơn lại toàn bộ mặt ngoài của bức tường đó sẽ là bao nhiêu?

Giải rút gọn:

Diện tích cần sơn là diện tích của hình chữ nhật trừ đi diện tích của cổng parabol.

Chọn hệ tọa độ Oxy có gốc tọa độ O(0;0) tại chân bên trái của bức tường. Cổng parabol có hàm số có dạng:

Cổng cao 4,8m, cách chân tường 2m, vì vậy đồ thị hàm số của cổng parabol đi qua các điểm A(2;0) và B(4;4,8). Ta có:

Cổng parabol có phương trình dạng:

Diện tích cổng parabol là diện tích hình phẳng giới hạn bởi các đường x=2,x=6, trục hoành Ox và :

Diện tích bức tường là:

Diện tích cần sơn là:

Chi phí để sơn toàn bộ mặt ngoài tường:

Bài 13:

Cho khối tròn xoay như Hình 39

 a) Hình phẳng được giới hạn bởi các đường nào để khi quay quanh trục Ox ta được khối tròn xoay như Hình 39

b) Tính thể tích khối tròn xoay đó

Giải rút gọn:

a) Quan sát hình 39, ta thấy hình phẳng tạo bởi khối tròn xoay được giới hạn bởi các đường và trục hoành Ox.

b) Thể tích khối tròn xoay đó là: