TRẮC NGHIỆM

Câu 1: Cho hai biến cố độc lập A, B với P(A) = 0, 8 P(B) = 0, 25 Khi đó, P(A|B) bằng:

• A. 0,2.

• B. 0,8.

• C. 0,25.
• D. 0,75.

Câu 2: Nếu hai biến cố A, B thoả mãn P(B) = 0,6 P(A ∩ B) = 0,2 thì P(A|B) bằng:

• A.
• B.

• C.

• D.

Câu 3: Nếu hai biến cố A, B thoả mãn P(B) = 0,3 P(A|B) = 0,5 thì P(A ∩ B) bằng:

• A. 0,8.
• B. 0,2.
• C. 0,6.

• D. 0,15.

Câu 4: Có quả cầu được đánh số từ đến . Lấy ngẫu nhiên đồng thời hai quả cầu rồi nhân các số trên hai quả với nhau. Tính xác suất để tích nhận được là một số chia hết cho ?

• A. .

• B. .

• C. .
• D. .

Câu 5: Trong một khu phố có 100 nhà, tại đó có 60 nhà gắn biển số chẵn và 40 nhà gắn biển số lẻ. Bên cạnh đó, có 50 nhà gắn biển số chẵn và 20 nhà gắn biển số lẻ đều có ô tô. Chọn ngẫu nhiên một nhà trong khu phố đó. Xác suất nhà được chọn có ô tô, biết rằng nhà đó gắn biển số chẵn, là:

• A.
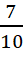
• B.
• C.

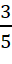
• D.

Câu 6: Trong một khu phố có 100 nhà, tại đó có 60 nhà gắn biển số chẵn và 40 nhà gắn biển số lẻ. Bên cạnh đó, có 50 nhà gắn biển số chẵn và 20 nhà gắn biển số lẻ đều có ô tô. Chọn ngẫu nhiên một nhà trong khu phố đó. Xác suất nhà được chọn gắn biển số lẻ, biết rằng nhà đó có ô tô, là:

• A.
• B.

• C.

• D.

Câu 7: Một nhóm học sinh gồm học sinh nam trong đó có An và học sinh nữ trong đó có Bình được xếp ngồi vào cái ghế trên một hàng ngang. Hỏi có bao nhiêu cách sắp xếp nam và nữ ngồi xen kẽ, đồng thời An không ngồi cạnh Bình?

• A. . 
• B. .

• C. . 

• D. .

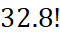Câu 8: Có học sinh, gồm học sinh lớp 12A và học sinh lớp 12B tham gia một trò chơi. Để thực hiện trò chơi, người điều hành ghép ngẫu nhiên học sinh thành cặp. Xác suất để không có cặp nào gồm hai học sinh cùng lớp bằng

• A. . 
• B. . 

• C. . 

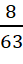• D. .

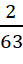Câu 9: Một phòng học môn Tin học có 40 máy tính được đánh số từ 1 đến 40, các máy cùng loại và cùng màu, mỗi máy được đánh một số khác nhau. Trong phòng học đó, xác suất chọn được một máy tính đã cài đặt phần mềm lập trình Python được đánh số chẵn và được đánh số lẻ lần lượt là 0,375 và 0,45. Bạn Nam chọn ngẫu nhiên một máy tính trong phòng học đó. Xác suất bạn Nam chọn được máy tính đã cài đặt phần mềm lập trình Python, biết rằng máy tính đó được đánh số lẻ, là:

• A.  
• B.

• C.

• D.

Câu 10: Một phòng học môn Tin học có 40 máy tính được đánh số từ 1 đến 40, các máy cùng loại và cùng màu, mỗi máy được đánh một số khác nhau. Trong phòng học đó, xác suất chọn được một máy tính đã cài đặt phần mềm lập trình Python được đánh số chẵn và được đánh số lẻ lần lượt là 0,375 và 0,45. Bạn Nam chọn ngẫu nhiên một máy tính trong phòng học đó. Xác suất bạn Nam chọn được máy tính đánh số chẵn, biết rằng máy tính đó đã cài đặt phần mềm lập trình Python, là:

• A.

• B.

• C.
• D.

Câu 11: Trong một đợt thi chứng chỉ hành nghề có 160 cán bộ tham gia, trong đó có 84 nam và 76 nữ. Khi công bố kết quả của kì kiểm tra đó, có 59 cán bộ đạt loại giỏi, trong đó có 30 cán bộ nam và 29 cán bộ nữ. Chọn ra ngẫu nhiên một cán bộ. Tính xác suất để cán bộ được chọn ra đạt loại giỏi, biết rằng cán bộ đó là nữ (làm tròn kết quả đến hàng phần trăm).

• A. 0,28
• B. 0,62

• C. 0,38

• D. 0,72

Câu 12: Một hộp đựng 5 quả bóng màu vàng và 3 quả bóng màu trắng, các quả bóng có kích thước và khối lượng như nhau. Lấy ngẫu nhiên lần thứ nhất một quả bóng (không hoàn lại), rồi lần thứ hai lấy một quả bóng khác. Tính xác suất để lần thứ nhất lấy được quả bóng màu vàng, lần thứ hai lấy được quả bóng màu trắng.

• A.

• B.

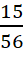
• C.
• D.

Câu 13: Một hộp đựng 24 chai nước giải khát có hình dạng và kích thước như nhau, trong đó có 2 chai nước giải khát ghi giải thưởng “Bạn nhận được thêm một chai nước giải khát". Chọn ra ngẫu nhiên lần lượt (không hoàn lại) hai chai nước trong hộp. Tính xác suất để cả hai chai đều ghi giải thưởng.

• A.

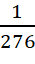
• B.
• C.
• D.

Câu 14: Một công ty có hai chi nhánh. Sản phẩm của chi nhánh I chiếm 54% tổng sản phẩm của công ty. Trong quá trình sản xuất phân loại, có 75% sản phẩm của công ty đạt loại A, trong đó có 65% của chi nhánh I. Chọn ngẫu nhiên một sản phẩm của công ty. Tính xác suất sản phẩm được chọn đạt loại A, biết rằng sản phẩm được chọn của chi nhánh I (làm tròn kết quả đến hàng phần mười).

• A. 0,9

• B. 0,65
• C. 0,54
• D. 0,4875

Câu 15: Trong buổi sinh hoạt nhóm của lớp, tổ một có học sinh gồm 4 học sinh nữ trong đó có Dung và 8 học sinh nam trong đó có Hải. Chia tổ thành 3 nhóm, mỗi nhóm gồm 4 học sinh và phải có ít nhất 1 học sinh nữ. Tính xác suất để Dung và Hải thuộc cùng một nhóm

• A. . 
• B. . 
• C. . 

• D. .

Câu 16: Có học sinh gồm học sinh trường A, học sinh trường B và học sinh trường C sắp xếp trên một hàng dọc. Xác suất để được cách cách sắp xếp mà hai học sinh trường C thì một em ngồi giữa hai học sinh trường A và một em ngồi giữa hai học sinh trường B là

• A. . 

• B. . 

• C. .
• D. .

Câu 17: Một lớp học có 30 học sinh nam và 10 học sinh nữ. Giáo viên chủ nhiệm cần chọn một ban cán sự lớp gồm có 3 học sinh. Tính xác suất để ban cán sự lớp có cả nam và nữ.

• A. .
• B. .

• C. .

• D. .

Câu 18: Hộp thứ nhất chứa 3 bi đỏ và 4 bi xanh, hộp thứ 2 chứa 2 bi đỏ và 5 bi xanh. Chuyển ngẫu nhiên 1 viên bi tứ hộp thứ nhất sang hộp thứ hai, rồi lấy ngẫu nhiên một viên bi từ hộp thứ hai ra. Tính xác suất để viên bi được lấy ra ở hộp thứ hai là màu đỏ.

• A.

• B.

• C.
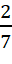
• D.

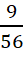
Câu 19: THÔNG và MINH tham gia trò chơi chiếc hộp may mắn, trong hộp kín đựng 6 tờ tiền mệnh giá đồng và 4 tờ tiền mệnh giá đồng được sắp xếp một cách lộn xộn, mỗi người lấy một tờ tiền từ hộp đó, xem đó là phần thưởng và cầm lấy, rồi vễ chỗ. THÔNG chơi lượt đầu tiên, lấy ngẫu nhiên một tờ tiền bất kỳ sau đó đến lượt MINH lấy ngẫu nhiên một tờ tiền bất kỳ từ hộp đó. Tính xác suất để MINH lấy được tờ tiền mệnh giá đồng.

• A. .
• B. .

• C. .

• D. .

Câu 20: Cho tập gồm 20 số tự nhiên từ 1 đến 20. Lấy ngẫu nhiên ba số thuộc . Xác suất để ba số lấy được lập thành một cấp số cộng là

• A. . 

• B. .

• C. .
• D. .