1. PHÉP CỘNG HAI ĐA THỨC MỘT BIẾN 

HĐKP1:

Chu vi của hình vuông là: 4x.

Chu vi của hình chữ nhật: 2.x.(x+1).

Tổng chu vi của hình vuông và hình chữ nhật là: 4x + 2x(x+1)

=> Kết luận:

Để cộng hai đa thức một biến, ta có thể thực hiện theo một trong hai cách sau:

Cách 1: Nhóm các đơn thức cùng lũy thừa của biến rồi thực hiện phép cộng.

Cách 2: Sắp xếp các các đơn thức của hia đa thức cùng theo thứ tự lũy thừa tăng dần (hoặc giảm dần) của biến và đặt tính dọc sao cho lũy thừa giống nhau ở hai đa thức thẳng cột với nhau, rồi thực hiện cộng theo cột.

Thực hành 1: 

Cách 1: 

P(x) + Q(x) 

= $7x^{3} – 8x + 12 + 6x^{2} – 2x^{3}+3x – 5$

= $(7x^{3}– 2x^{3}) + 6x^{2} +(-8x+ 3x) +(12 – 5)$

= $5x^{3} + 6x^{2} +-5x + 7$

Cách 2: 

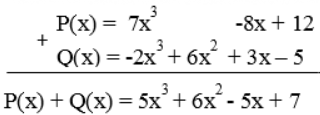
2. PHÉP TRỪ HAI ĐA THỨC MỘT BIẾN 

HĐKP2:

Diện tích hình chữ nhật là: 4x.2x = 8x$^{2}$

Diện tích hình vuông là: x$^{2}$

Diện tích phần được tô màu vàng là: $8x^{2}-x^{2}$

=> Kết luận:

Để trừ hai đa thức một biến, ta có thể thực hiện theo một trong hai cách sau:

- Cách 1: Nhóm các đơn thức cùng lũy thừa của biến rồi thực hiện phép trừ

- Cách 2: Sắp xếp các đơn thức của hai đa thức cùng theo thứ tự lũy thừa tăng dần (hoặc giảm dần) của biến và đặt tính dọc sao  cho lũy thừa giống nhau ở hai đa thức thẳng cột với nhau, rồi thực hiện trừ theo cột.

Thực hành 2:

Cách 1: 

P(x) – Q(x) 

= $(2x^{3} – 9x^{2}+ 5) – (-2x^{2} -9x^{2} + 5) – (-2x^{2} – 4x^{3} + 7x)$

= $2x^{3} – 9x^{2}+ 5 + 2x^{2}+ 4x^{3}-7x = (2x^{3} + 4x^{3}) + (– 9x^{2} + 2x^{2} ) – 7x + 5$

= $6x^{3} – 7x^{2} -7x + 5$

Cách 2: 

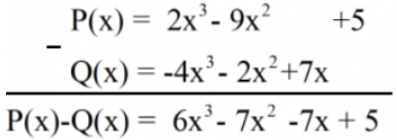
3. TÍNH CHẤT CỦA PHÉP CỘNG ĐA THỨC MỘT BIẾN

=> Kết luận:

Cho A, B, C là các đa thức một biến với cùng một biến số. Ta có:

• A + B = B + A

• A + (B + C) = (A + B) + C

Thực hành 3:

$(x-4)+[(x^{2}+2x)+(7-x)]$

$=x-4+x^{2}+2x+7-x$

$=x^{2}+2x+3$