CHƯƠNG I. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC

BÀI 2. CÔNG THỨC LƯỢNG GIÁC

1. CÔNG THỨC CỘNG

Hoạt động 1:

a) Ta có: a-b=$\frac{\pi }{4}$-$\frac{\pi }{6}$=$\frac{\pi }{12}$ nên 

cos (a-b) =cos $\frac{\pi }{12}$ =$\frac{\sqrt{6}+\sqrt{2}}{4}$

cos a .cos b =sin a.sin b   

=cos $\frac{\pi }{4}$.cos $\frac{\pi }{6}$ +sin $\frac{\pi }{4}$ .sin $\frac{\pi }{6}$  

=$\frac{\sqrt{2}}{2}$.$\frac{\sqrt{3}}{2}$+$\frac{\sqrt{2}}{2}$.$\frac{1}{2}$ 

=$\frac{\sqrt{6}}{4}$+$\frac{\sqrt{2}}{4}$=$\frac{\sqrt{6}+\sqrt{2}}{4}$ 

Vậy 

cos(a – b)=cos a cos b+sin a sin b.

b) Ta có: cos(a + b) = cos[a – (– b)]

= cos a cos(– b) + sin a sin(– b) 

Mà 

cos(– b) = cos b, sin(– b) = – sin b  (hai góc đối nhau).

Do đó, 

cos(a + b)= cos a cos b + sin a . (– sin b)  

= cos a cos b – sin a sin b. 

c) Ta có: 

sin (a-b) =cos [$\frac{\pi }{2}$-(a-b)]

=cos [($\frac{\pi }{2}$-a)+b]

=cos ($\frac{\pi }{2}$-a).cos b-sin ($\frac{\pi }{2}$-a).sin b   

=sin a .cos b-cos a.sin b  

(do cos cos($\frac{\pi }{2}$-a) =sin sina ;

sin ($\frac{\pi }{2}$-a )=cos a . 

Vậy sin(a – b) = sin a cos b – cos a sin b.

Công thức:

cos (a-b) =cos a cos b +sin a sin b

cos (a+b)=cos a cos b-sin a sin b 

sin (a-b)=sin a cos b-cos a sin b  

sin (a+b)=sin a cos b+cos a sin b  

tan (a-b) = $\frac{tan a - tan b}{1 + tan a.tan b}$ 

tan (a+b) = $\frac{tan a + tan b}{1 - tan a.tan b}$ 

(giả thiết các biểu thức đều có nghĩa).

Ví dụ 1: (SGK – tr.17).

Hướng dẫn giải (SGK – tr.18).

Ví dụ 2: (SGK – tr.18).

Hướng dẫn giải (SGK – tr.18).

Luyện tập 1:

a) Ta có: 

VP=$\sqrt{2}$sin (x-$\frac{\pi }{4}$) 

=$\sqrt{2}$(sin x cos $\frac{\pi }{4}$ -cos x sin $\frac{\pi }{4}$)

=$\sqrt{2}$ sin x .$\frac{\sqrt{2}}{2}$-$\sqrt{2}$cos x .$\frac{\sqrt{2}}{2}$ 

=sin x-cos x=VT (đpcm).

b) Ta có: 

VT=tan ($\frac{\pi }{4}$-x) = $\frac{tan \frac{\pi }{4} - tan x}{1 + tan \frac{\pi }{4}.tan x}$ =VP 

(do tan $\frac{\pi }{4}$ =1).

Vận dụng 1:

Ta có: f(t)=f$_{1}$(t)+f$_{2}$(t)

=5sin t +5cos t =5(sin t +cos t ) 

Theo Ví dụ 2 trang 18 SGK Toán lớp 11 Tập 1, ta chứng minh được:

sin t +cos t =$\sqrt{2}$sin (1+$\frac{\pi }{4}$)  

Do đó, f(t)=5$\sqrt{2}$sin (t+$\frac{\pi }{4}$)

Vậy âm kết hợp viết được dưới dạng f(t)=ksin (t+$\varphi $), trong đó biên độ âm k=5$\sqrt{2}$ và pha ban đầu của sóng âm là $\varphi $=$\frac{\pi }{4}$

2. CÔNG THỨC NHÂN ĐÔI

Hoạt động 2:

+) sin 2a = sin(a + a)

= sin a cos a + cos a sin a  

= sin a cos a + sin a cos a 

= 2 sin a cos a. 

+) cos 2a =cos (a+a)

= cos a cos a – sin a sin  

= a - a

Mà a + a =1, 

suy ra =1 – a và

= 1 – sin2 a. 

Do đó, cos 2a = a – a  

=2a – 1=1 –2a .

+) tan 2a=tan (a+a) 

= $\frac{tantan a + tantan a}{1 - tantan a.tantan a}$ =$\frac{2tantan a }{1 - a}$  

Công thức nhân đôi

sin 2a =2sin a cos a  

cos 2a =a - a   

              =2a -1=1- 2a   

tan 2a =$\frac{2tan a }{1 - a}$   .

Ví dụ 3: (SGK – tr.18).

Hướng dẫn giải (SGK – tr.18).

Công thức hạ bậc

a =$\frac{1+ coscos 2a}{2}$

a =$\frac{1- coscos 2a}{2}$ 

Luyện tập 2

Ta có: $\frac{\sqrt{2}}{2}$=coscos$\frac{\pi }{4}$ =coscos(2.$\frac{\pi }{8}$)

=2$\frac{\pi }{8}$ -1 

Suy ra 2$\frac{\pi }{8}$ =1+$\frac{\sqrt{2}}{2}$. Do đó:

$\frac{\pi }{8}$=$\frac{2+\sqrt{2}}{4}$ 

Vì cos $\frac{\pi }{8}$ >0 nên suy ra cos $\frac{\pi }{8}$ =$\frac{\sqrt{2+\sqrt{2}}}{2}$

Vì cos $\frac{\pi }{8}$ >0 nên suy ra cos $\frac{\pi }{8}$ =$\frac{\sqrt{2+\sqrt{2}}}{2}$

3. CÔNG THỨC BIỂN ĐỔI TÍCH THÀNH TỔNG

Hoạt động 3:

a) Ta có: 

cos(a + b)=cos a cos b – sin a sin b  (1);

cos(a–b)=cos a cos b+sin a sin b  (2).

Lấy (1) và (2) cộng vế theo vế, ta được: cos(a+b)+cos(a –b)=2 cos a cos b.

Từ đó suy ra:

cos a cos b=$\frac{1}{2}$[cos(a+b)+cos(a – b)]. 

Lấy (2) trừ vế theo vế cho (1), ta được: cos(a–b)–cos(a+b)=2 sin a sin b.

Từ đó suy ra:

sin a sin b=$\frac{1}{2}$[cos(a –b) –cos(a+b)]. 

b) Ta có: 

sin(a+b)=sin a cos b+cos a sin b  (3); 

sin(a – b)=sin a cos b –cos a sin b   (4). 

Lấy (3) và (4) cộng vế theo vế, ta được: sin(a+b)+sin(a – b)=2sin a cos b.

Từ đó suy ra:

sin a cos b=$\frac{1}{2}$[sin(a+b)+sin(a – b)]. 

Công thức biến đổi tích thành tổng

cos a cos b=$\frac{1}{2}$[cos(a+b)+cos(a – b)]. 

sin a sin b=$\frac{1}{2}$[cos(a – b) – cos(a + b)]. 

sin a cos b=$\frac{1}{2}$[sin(a+b)+sin(a – b)]. 

Ví dụ 4: (SGK – tr.19).

Hướng dẫn giải: (SGK – tr.19).

Luyện tập 3:

Ta có:

A=cos 75$^{\circ}$ cos 15$^{\circ}$  

=$\frac{1}{2}$[cos 75$^{\circ}$-15$^{\circ}$+cos (75$^{\circ}$+15$^{\circ}$) 

=$\frac{1}{2}$cos 60$^{\circ}$+cos 90$^{\circ}$  

=$\frac{1}{2}$.$\frac{1}{2}$+0=$\frac{1}{4}$ 

B=sin $\frac{5\pi }{12}$ cos $\frac{7\pi }{12}$  

=$\frac{1}{2}$[sin($\frac{5\pi }{12}$-$\frac{7\pi }{12}$)+sin ($\frac{5\pi }{12}$+$\frac{7\pi }{12}$ ) 

=$\frac{1}{2}$(sin(-$\frac{\pi }{6}$)+sin $\pi $)

=$\frac{1}{2}$(-sin $\frac{\pi }{6}$+sin $\pi $)

=$\frac{1}{2}$(-$\frac{1}{2}$+0)=-$\frac{1}{4}$

4. CÔNG THỨC BIẾN ĐỔI TỔNG THÀNH TÍCH

Hoạt động 4:

cos a cos b=$\frac{1}{2}$[cos(a+b)+cos(a – b)] (1) 

sin a sin b=$\frac{1}{2}$[cos(a – b) – cos(a + b)] (2)

sin a cos b=$\frac{1}{2}$[sin(a+b)+sin(a – b)] (3)

Đặt u=a – b; v=a+b.

Ta có: u+v=(a-b)+(a+b)=2a

Và u-v=(a-b)-(a+b)=-2b

Suy ra, a=$\frac{u+v}{2}$;b=-$\frac{u-v}{2}$

Khi đó:

+ (1) trở thành:

cos $\frac{(u+v)}{2}$ cos(-$\frac{u-v}{2}$) =$\frac{1}{2}$cos u +cos v  

<=> cos u+cos v=2cos $\frac{u+v}{2}$cos $\frac{u-v}{2}$  (do cos (-$\frac{u-v}{2}$)=cos $\frac{u-v}{2}$).

+) (2) trở thành:

sin $\frac{u+v}{2}$ sin (-$\frac{u-v}{2}$) =$\frac{1}{2}$(cos u-cos v) 

⇔ cos u-cos v=-2sin $\frac{u+v}{2}$sin $\frac{u-v}{2}$

(do sin -$\frac{u-v}{2}$=-sin $\frac{u-v}{2}$  ).

+) (3) trở thành:

sin $\frac{u+v}{2}$cos -$\frac{u-v}{2}$=$\frac{1}{2}$(sin u+sin v)      

⇔ sin u+sin v=2sin $\frac{u+v}{2}$cos $\frac{u-v}{2}$.

Công thức biến đổi tổng thành tích

cos u+cos v=2cos $\frac{u+v}{2}$cos $\frac{u-v}{2}$ 

cos u -cos v=-2sin $\frac{u+v}{2}$sin $\frac{u-v}{2}$ 

sin u+sin v=2sin $\frac{u+v}{2}$cos $\frac{u-v}{2}$ 

sin u-sin v=2cos $\frac{u+v}{2}$sin $\frac{u-v}{2}$    

Ví dụ 5: (SGK – tr.20).

Hướng dẫn giải: (SGK – tr.20).

Câu hỏi:

a) cos x+cos 2x+cos 3x+cos 4x

=(cos 4x +cos x) + (cos 3x+cos 2x )

= 2cos $\frac{5x}{2}$ cos $\frac{3x}{2}$ +2cos $\frac{5x}{2}$ cos $\frac{x}{2}$  

=2cos $\frac{5x}{2}$ (cos $\frac{3x}{2}$+cos $\frac{x}{2}$)  

= 4cos $\frac{5x}{2}$ cos x cos $\frac{x}{2}$

=4cos x cos $\frac{5x}{2}$ cos $\frac{x}{2}$  

b) sin a +sin b +sin (a+b)

=2sin $\frac{a+b}{2}$ cos $\frac{a-b}{2}$ +2sin $\frac{a+b}{2}$ cos $\frac{a+b}{2}$ 

= 2sin $\frac{a+b}{2}$ (cos $\frac{a-b}{2}$ +cos $\frac{a+b}{2}$ ) 

=2sin $\frac{a+b}{2}$ .2cos $\frac{a}{2}$ cos (-$\frac{b}{2}$)  

= 4sin $\frac{a+b}{2}$ cos $\frac{a}{2}$ cos $\frac{b}{2}$

Luyện tập 4:

Ta có: B=cos $\frac{\pi }{9}$+cos $\frac{5\pi }{9}$+cos $\frac{11\pi }{9}$  

=(cos $\frac{\pi }{9}$+cos $\frac{11\pi }{9}$)+cos $\frac{5\pi }{9}$    

=2cos $\frac{\frac{\pi }{9}+\frac{11\pi }{9} }{2}$cos $\frac{\frac{\pi }{9}-\frac{11\pi }{9} }{2}$+cos $\frac{5\pi }{9}$    

=2cos $\frac{2\pi }{3}$cos (-$\frac{5\pi }{9}$)+cos $\frac{5\pi }{9}$     

=2cos $\frac{2\pi }{3}$cos $\frac{5\pi }{9}$+cos $\frac{5\pi }{9}$     

=2.(-$\frac{1}{2}$)cos $\frac{5\pi }{9}$+cos $\frac{5\pi }{9}$   

=-cos $\frac{5\pi }{9}$+cos $\frac{5\pi }{9}$=0 

Vận dụng 2:

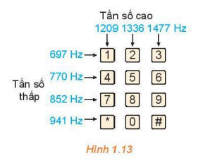
a) Quan sát Hình 1.13, ta nhận thấy khi nhấn phím 4, âm thanh được tạo ra có tần số thấp f$_{1}$= 770 Hz và tần số cao f$_{2}$=1 209 Hz.

Khi đó, hàm số mô hình hóa âm thanh được tạo ra khi nhấn phím 4 là:

y=sin 2$\pi $ . 770t +sin 2$\pi $.1 209t

hay:

y=sin(1540$\pi $t)+sin(2418$\pi $t). 

b) Ta có:

sin (1540$\pi $t)+sin (2418$\pi $t)    

=2sin $\frac{1540\pi t+2418\pi t}{2}$cos $\frac{1540\pi t-2418\pi t}{2}$

=2sin (1979 $\pi $t)cos (-439$\pi $t) 

=2sin (1979 $\pi $t)cos (439$\pi $t) 

Vậy ta có hàm số:  y=2sin (1979$\pi $t)cos (439$\pi $t).