CHƯƠNG I: HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC

BÀI 5: PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN

1. PHƯƠNG TRÌNH TƯƠNG ĐƯƠNG 

HĐKP 1

a) Tập nghiệm của phương trình x-1=0 là S$_{1}$={1}.

Tập nghiệm của phương trình x$^{2}$-1=0 là S$_{2}$={-1;1}.

Tập nghiệm của phương trình $\sqrt{2x^{2}-1}$=x là S$_{3}$={1}.

Ta có S$_{1}$=S$_{3} \neq $S$_{2}$.

Kết luận

 Hai phương trình được gọi là tưong

 đưong nếu chúng có cùng tập nghiệm.

 Ví dụ 1 (SGK -tr.34)

 Chú ý:

- Một số phép biến đổi tương đương thường sử dụng 

+ Cộng hoặc trừ hai vế của phương trình cùng với một số hoặc cùng một biểu thức mà không làm thay đổi điều kiện của phương trình.

+ Nhân hoặc chia hai vế của phương trình với cùng một số khác 0 hoặc cùng một biểu thức luôn có giá trị khác 0 mà không thay đổi điều kiện của phương

trình.

- Để chỉ sự tương đương của các phương trình, dùng kí hiệu $\Leftrightarrow $.

Thực hành 1

Phép biến đổi đầu tiên không là biến đổi tương đương, do khi chia cả hai vế của phương trình cho x=0 thì làm mất đi nghiệm này. 

Phương trình đầu tiên có hai nghiệm x=0 và x=2, còn phương trình thứ hai chỉ có nghiệm x=0.

2. PHƯƠNG TRÌNH SIN X = M

HĐKP 2

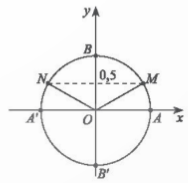
a) Không có giá trị nào của x để sin⁡x=1,5 vì -1≤sin⁡x≤1 với mọi x∈R.

b) Đường thẳng vuông góc trục sin tại điểm 0,5 cắt đường tròn lượng giác tại hai điểm M và N. Do đó M và N là điểm biểu diễn các góc lượng giác x có ⁡sin⁡x=0,5. 

Các góc lượng giác đó lần lượt là $\frac{\pi }{6}$+k2π và $\frac{5\pi }{6}$+k2π,k∈Z.

Kết luận

Xét phương trình sin⁡x=m 

+) Nếu |m|>1 thì phương trình vô nghiệm.

+) Nếu |m|≤1 thì phương trình có nghiệm

x=α+k2π, k∈Z

Và x=π-α+k2π, k∈Z

Với  α∈[-$\frac{\pi }{2}$;$\frac{\pi }{2}$] sao cho sin =m.

Chú ý:

a) Một số trường hợp đặc biệt:

• sin⁡x=0⇔x=kπ,k∈Z.

• sin⁡x=1⇔x=$\frac{\pi }{2}$+k2π,k∈Z.

• sin x =-1⇔x=-$\frac{\pi }{2}$+k2π,k∈Z

b) sinsinu =sinsinv

<=> [u=v+k2π u=π-v+k2π (k∈Z)

c)sinsinx =sinsina

<=> [x=a$^{\circ}$+k360$^{\circ}$ x=180$^{\circ}$-a$^{\circ}$+k360$^{\circ}$ (k∈Z)

Ví dụ 2 (SGK -tr.35)

Thực hành 2

a) sinsinx =$\frac{\sqrt{3}}{2}$ <=> sinsinx =sinsin$\frac{\pi }{3}$

⇔x=$\frac{\pi }{3}$+k2π,k∈Z hoặc x=$\frac{2\pi }{3}$+k2π,k∈Z.

b) sin⁡(x+30$^{\circ}$)=sin(⁡x+60$^{\circ}$)

⇔x+30$^{\circ}$=x+6$^{\circ}$0+k360$^{\circ}$,k∈Z hoặc

x+30$^{\circ}$=180$^{\circ}$-x-60$^{\circ}$+k360$^{\circ}$,k∈Z

⇔x+30$^{\circ}$=120$^{\circ}$-x+k360$^{\circ}$,k∈Z

⇔x=45$^{\circ}$+k180$^{\circ}$,k∈Z.

3. PHƯƠNG TRÌNH COS X = M

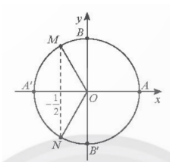
Đường thẳng vuông góc trục côsin tại điểm -$\frac{1}{2}$ cắt đường tròn lượng giác tại hai điểm M và N. Do đó M và N là điểm biểu diễn các góc lượng giác x cos⁡cos⁡x=-$\frac{1}{2}$. 

Các góc lượng giác đó lần lượt là $\frac{2\pi }{3}$+k2π và -$\frac{2\pi }{3}$+k2π,k∈Z.

Kết luận

Xét phương trình cos⁡x=m 

+) Nếu |m|>1 thì phương trình vô nghiệm.

+) Nếu |m|≤1 thì phương trình có nghiệm

x=α+k2π, k∈Z

Và x=-α+k2π, k∈Z

Với  α∈[0;π] sao cho cos =m.

Chú ý:

a) Một số trường hợp đặc biệt:

• cos⁡x=0⇔x=$\frac{\pi }{2}$+kπ,k∈Z.

• cos⁡x=1⇔x=k2π,k∈Z.

• cos⁡x=-1⇔x=π+k2π,k∈Z

b)
coscosu =cos⁡v⇔[u=v+k2π v=-v+k2π (k∈Z)

c) 

cos⁡x=cos⁡a$^{\circ}$[x=a$^{\circ}$+k360$^{\circ}$ x=-a$^{\circ}$+k360$^{\circ}$ (k∈Z)

Ví dụ 3 (SGK -tr.37)

Thực hành 3

a) cos⁡x=-3 vô nghiệm;

b) coscos x =coscos 15$^{\circ}$

⇔x=15$^{\circ}$+k360$^{\circ}$,k∈Z hoặc

x=-15$^{\circ}$+k360$^{\circ}$,k∈Z.

c) coscos( x+$\frac{\pi }{12}$) =coscos($\frac{3\pi }{12}$)

⇔x+$\frac{\pi }{12}$=$\frac{3\pi }{12}$+k2π,k∈Z hoặc

x+$\frac{\pi }{12}$=-$\frac{3\pi }{12}$+k2π,k∈Z

⇔x=$\frac{\pi }{6}$+k2π,k∈Z hoặc x=-$\frac{\pi }{3}$+k2π,k∈Z

4. ĐƯỜNG TRÒN LƯỢNG GIÁC

HĐKP 4

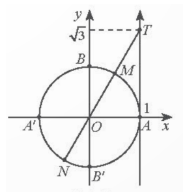
Đường thẳng đi qua gốc tọa độ và điểm T(1;$\sqrt{3}$) cắt đường tròn lượng giác tại hai điểm M và N. Do đó M và N là điểm biểu diễn các góc lượng giác x có tan x=$\sqrt{3}$. Công thức tổng quát của các góc lượng giác đó là $\frac{\pi }{3}$+kπ,k∈Z.

Kết luận

Với mọi số thực m, phương trình tan x=m có nghiệm 

x=α+kπ(k∈Z).

Với α∈(-$\frac{\pi }{2}$;$\frac{\pi }{2}$) sao cho tan α=m.

Chú ý:

tan⁡x=tan⁡a$^{\circ}$⇔x=a$^{\circ}$+k180$^{\circ}$ (k∈Z).

Ví dụ 4 (SGK -tr.38)

Thực hành 4

a) tan⁡x=0⇔x=kπ,k∈Z.

b) tantan( 30$^{\circ}$-3x) =tantan75$^{\circ}$

<=> 30$^{\circ}$-3x=75$^{\circ}$+k180$^{\circ}$,k∈Z

⇔x=-15$^{\circ}$+k60$^{\circ}$,k∈Z

5. PHƯƠNG TRÌNH COT X = M

HĐKP 5

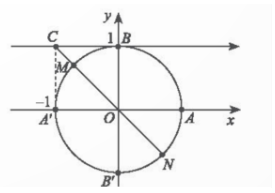
Đường thẳng đi qua gốc toạ độ và điểm C(-1;1) cắt đường tròn lượng giác tại hai điểm M và N. Do đó M và N là điểm biểu diễn các góc lương giác xcos⁡cot⁡x=-1.

Công thức tổng quát của các góc lượng giác đó là -$\frac{\pi }{4}$+kπ,k∈Z.

Kết luận

- Với mọi số thực , phương trình cot⁡x=m có nghiệm 

x=α+kπ(k∈Z)

với α∈(0;π) sao cho cot⁡α=m.

Chú ý

cot⁡x=cot⁡a$^{\circ}$⇔x=a$^{\circ}$+k180$^{\circ}$ (k∈Z).

Ví dụ 5 (SGK -tr.39)

Thực hành 5

a) cot⁡x=1⇔x=$\frac{\pi }{4}$+kπ,k∈Z;
b) cot(⁡3x+30$^{\circ}$)=tan⁡75$^{\circ}$⇔3x+30$^{\circ}$=75$^{\circ}$+k180$^{\circ}$,k∈Z
⇔x=15$^{\circ}$+k60$^{\circ}$,k∈Z.

6. GIẢI PHƯƠNG TRÌNH LƯỢNG GIÁC BẰNG MÁY TÍNH CẦM TAY

Ví dụ 6 (SGK -tr.40)

Chú ý:

Để giải phương trình  cotcot x=mm≠0 , ta giải phương trình tantan x=$\frac{1}{m}$.

Thực hành 6

a) cos⁡x=0,4⇔x≈1,16+k2π,k∈Z hoặc x≈-1,16+k2π,k∈Z.

b) tan⁡x=$\sqrt{3}$⇔x=$\frac{\pi }{3}$+kπ,k∈Z.

Vận dụng

Ta có |x|=10⇔17cos⁡5πt=10 hoặc 17cos⁡5πt=-10.

+) 17cos⁡5πt=10

coscos 5πt =$\frac{10}{17}$

⇔5πt≈0,94+k2π,k∈Z hoặc 5πt≈-0,94+k2π,k∈Z

⇔t≈0,06+0,4k,k∈Z hoăc t≈-0,06+0,4k,k∈Z.

+) 17coscos 5πt =-10

coscos 5πt =-$\frac{10}{17}$

⇔5πt≈2,2+k2π,k∈Z hoặc 5πt≈-2,2+k2π,k∈Z

⇔t≈0,14+0,4k,k∈Z hoặc t≈-0,14+0,4k,k∈Z.