Lý thuyết trọng tâm toán 11 cánh diều bài 3: Hàm số mũ. Hàm số lôgarit
Tổng hợp kiến thức trọng tâm toán 11 cánh diều bài 3: Hàm số mũ. Hàm số lôgarit. Tài liệu nhằm củng cố, ôn tập lại nội dung kiến thức bài học cho học sinh dễ nhớ, dễ ôn luyện. Kéo xuống để tham khảo
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
I. HÀM SỐ MŨ
1. Định nghĩa
HĐ1
a) Số tiền doanh nghiệp đó có được:
- Sau 1 năm: 1 000 000 000 + 1 000 000 000 . 6,2% = 1 062 000 000 (đồng)
- Sau 2 năm: 1 062 000 000 + 1 062 000 000 . 6,2% = 1 127 844 000 (đồng)
- Sau 3 năm: 1 127 844 000 + 1 127 844 000 . 6,2% = 1 197 770 328
b) Dự đoán công thức:
A = 1 000 000 000 . (1 + 6,2%)$^{n}$
Nhận xét: Tương ứng mỗi giá trị x với giá trị y = 1,062$^{x}$ xác định một hàm số, hàm số đó gọi là hàm số mũ cơ số 1,062.
Định nghĩa: Cho số thực a (a > 0, a ≠ 1). Hàm số y = a$^{x}$ được gọi là hàm số mũ cơ số a.
Tập xác định của hàm số mũ y = a$^{x}$ (a > 0, a ≠ 1) là R.
Ví dụ 1: (SGK – tr.39)
Hướng dẫn giải (SGK – tr.39)
Luyện tập 1
y = $0,5^{x}$; y = $(3\sqrt{3})^{x}$
2. Đồ thị và tính chất
HĐ2
a)
x | -1 | 0 | 1 | 2 | 3 |
y | $\frac{1}{2}$ | 1 | 2 | 4 | 8 |
b)
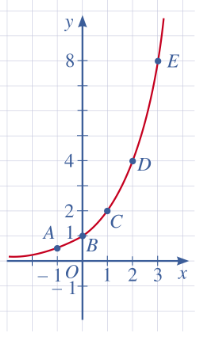
c) Tọa độ giao điểm của đồ thị y = 2$^{x}$ với trục tung là 0;1; Đồ thị không cắt trục hoành.
d) 2$^{x}$ = +∞ ; 2$^{x}$ =0
Hàm số y = 2$^{x}$ đồng biến trên R.
x | -∞ +∞ |
y | +∞ 0 |
Nhận xét: Đồ thị hàm số y = 2$^{x}$ là một đường cong liền nét, cắt trục tung tại điểm có tung độ bằng 1, nằm ở phía trên trục hoành và đi lên từ trái sang phải.
HĐ3
a)
x | -3 | -2 | -1 | 0 | 1 |
y | 8 | 4 | 2 | 1 | $\frac{1}{2}$ |
b)
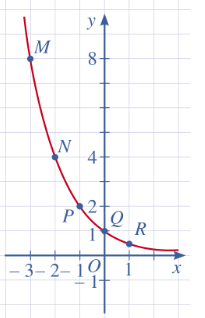
c) Tọa độ giao điểm của đồ thị hàm số y = $\left ( \frac{1}{2} \right )^{x}$ với trục tung là (0; 1)
Đồ thị hàm số y = $\left ( \frac{1}{2} \right )^{x}$ không cắt trục hoành.
d) $\left ( \frac{1}{2} \right )^{x}$ = 0; $\left ( \frac{1}{2} \right )^{x}$ = +∞
Hàm số y = $\left ( \frac{1}{2} \right )^{x}$ nghịch biến trên R.
x | -∞ +∞ |
y |
|
Nhận xét
Đồ thị hàm số y = $\left ( \frac{1}{2} \right )^{x}$ là một đường cong liền nét, cắt trục tung tại điểm có tung độ bằng 1, nằm ở phía trên trục hoành và đi xuông kẻ từ trái sang phải.
|
|
Nhận xét: Đồ thị hàm số y = a$^{x}$ (a > 0, a ≠ 1) là một đường cong liền nét, cắt trục tung tại điểm có tung độ bằng 1, nằm ở phía trên trục hoành và đi lên nếu a > 1, đi xuông nếu 0 < a < 1.
y = a$^{x}$ (a>1) | ||||
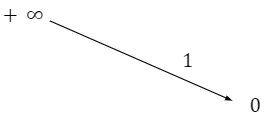
Tập xác định: R; tập giá trị: 0; +∞ Tính liên tục: Hàm số y = a$^{x}$ a>1 là hàm số liên tục trên R. Giới hạn đặc biệt: a$^{x}$ =0 ; a$^{x}$ = +∞ Sự biến thiên: Hàm số đồng biến trên R. Bảng biến thiên:
|
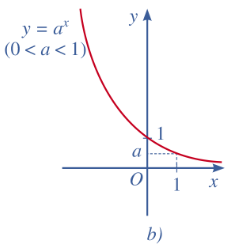
y = a$^{x}$ (0 < a < 1) | ||||
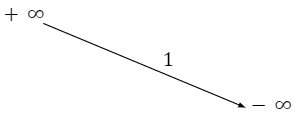
Tập xác định: R; tập giá trị: 0; +∞ Tính liên tục: Hàm số y=a$^{x}$ 0<a<1 là hàm số liên tục trên R. Giới hạn đặc biệt: a$^{x}$ =+∞ ;ax =0 Sự biến thiên: Hàm số nghịch biến trên R. Bảng biến thiên:
|
Chú ý:
Với mỗi N > 0, tồn tại duy nhất số sao cho a$^{\alpha }$ = N.

Ví dụ 2: (SGK – tr.42)
Hướng dẫn giải (SGK – tr.42)

Luyện tập 2
- Hàm số $\left ( \frac{1}{3} \right )^{x}$ là hàm số nghịch biến trên R.
- Vì hàm số $\left ( \frac{1}{3} \right )^{x}$ có cơ số 0 < $\frac{1}{3}$ < 1 nên ta có bảng biến thiên sau:
x | -∞ 0 +∞ |
y |
|
Đồ thị hàm số đi qua các điểm A(-2; 9), B(-1; 3), C(0; 1), D(1; 1/3)

Ví dụ 3: (SGK – tr.42)
Hướng dẫn giải (SGK – tr.42)
II. HÀM SỐ LÔGARIT
1. Định nghĩa
HĐ4
x | 1 | 3 | 9 | 27 |
y = log$_{3}$x | 0 | 1 | 2 | 3 |
Nhận xét: Tương ứng mỗi giá trị x dương với giá trị y = log$_{a}$x xác định một hàm số, hàm số đó gọi là hàm số lôgarit cơ số 3.
Định nghĩa; Cho số thực a (a > 0, a ≠ 1). Hàm số y = log$_{a}$x được gọi là hàm số loogarit cơ số a.
Tập xác định của hàm số lôgarit y = log$_{a}$x (a > 0, a ≠ 1) là (0; +∞).
Ví dụ 4: (SGK – tr. 43)
Hướng dẫn giải (SGK – tr.42)
Luyện tập 3
(1) $y=log_{4}x$
(2)$y=log(x+1)$
2. Đồ thị và tính chất
HĐ5
a)
x | 0,5 | 1 | 2 | 4 | 8 |
y | -1 | 0 | 1 | 2 | 3 |
b)
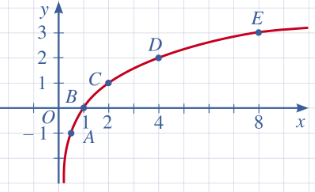
c) Tọa độ giao điểm của đồ thị hàm số y = log$_{2}$x với trục hoành là (1; 0)
Đồ thị hàm số đó không cắt trục tung.
d) $\lim_{x \rightarrow 0^{+}} log_{2}x=-\infty, \lim_{x \rightarrow +\infty } log_{2}x=+\infty$
Hàm số đồng biến trên $(0; +\infty)$

Nhận xét: Đồ thị hàm số y = log$_{2}$x là một đường cong liền nét, cắt trục hoành tại điểm có hoành độ bằng 1, nằm ở phía bên phải trục tung và đi lên kể từ trái sang phải.
HĐ6
a)
x | 0,5 | 1 | 2 | 4 | 8 |
y | 1 | 0 | -1 | -2 | -3 |
b)
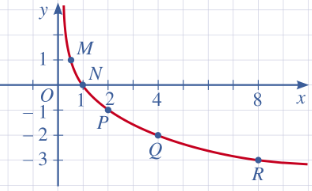
c) Tọa độ giao điểm của đồ thị hàm số y = x với trục hoành là (1; 0)
+ Đồ thị hàm số không cắt trục tung.
d) x = 0 ; x = -∞
Hàm số y = x nghịch biến trên (0;+∞).
Bảng biến thiên

Nhận xét: Đồ thị hàm số x là một đường cong liền nét, cắt trục hoành tại điểm có hoành độ bằng 1, nằm phía bên phải tục tung và đi xuống kể từ trái sang phải.
Ghi nhớ; Đồ thị hàm số y = x (a > 0, a ≠ 1) là một đường cong liền nét, cắt trục hoành tại điểm có hoành độ bằng 1, nằm ở phía bên phải trục tung và đi lên nếu a > 1, đi xuống nếu 0 < a < 1.
|
|
Nhận xét: Cho hàm số lôgarit y = x với a > 0, a ≠ 1.
y = x với a > 1 | ||||
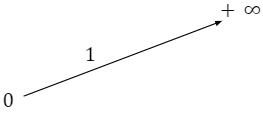
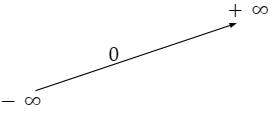
+ Tập xác định: (0; +∞); tập giá trị: R + Tính liên tục: Hàm số y=x (a>1) là hàm số liên tục trên khoảng (0;+∞) + Giới hạn đặc biệt: x = -∞ ; x = +∞ + Sự biến thiên: Hàm số đồng biến trên (0; +∞). + Bảng biến thiên
|
y= x với 0 < a < 1 | ||||
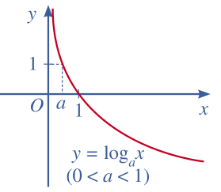
+ Tập xác định: (0;+∞); tập giá trị: R + Tính liên tục: Hàm số y = x (0 < a < 1) là hàm số liên tục trên khoảng (0;+∞). + Giới hạn đặc biệt: x = +∞ ; x =-∞ + Sự biến thiên: Hàm số nghịch biến trên (0;+∞) + Bảng biến thiên
|
Ví dụ 5: (SGK – tr46)
Hướng dẫn giải (SGK – tr.46)
Luyện tập 4
Vì hàm số y = x có cơ số 0 < $\frac{1}{3}$ < 1 nên ta có bảng biến thiên như sau:
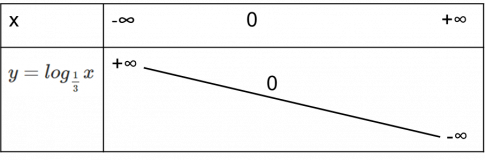
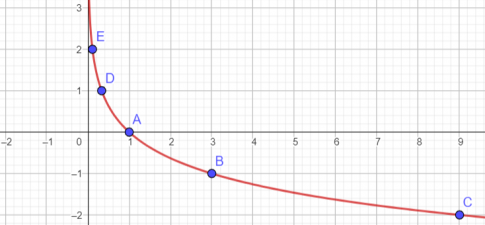
Đồ thị hàm số $y=log_{\frac{1}{3}}x$ là đường cong đi qua các điểm A(1;0), B(3; -1), C(9;-2), D($\frac{1}{3}$; 1)
Ví dụ 6: (SGK – tr.46)
Hướng dẫn giải (SGK – tr.46)
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
Nội dung quan tâm khác
Thêm kiến thức môn học
Giải bài tập những môn khác
Giải sgk lớp 11 KNTT
Giải sgk lớp 11 CTST
Giải sgk lớp 11 cánh diều
Giải SBT lớp 11 kết nối tri thức
Giải SBT lớp 11 chân trời sáng tạo
Giải SBT lớp 11 cánh diều
Giải chuyên đề học tập lớp 11 kết nối tri thức
Giải chuyên đề toán 11 kết nối tri thức
Giải chuyên đề ngữ văn 11 kết nối tri thức
Giải chuyên đề vật lí 11 kết nối tri thức
Giải chuyên đề hóa học 11 kết nối tri thức
Giải chuyên đề sinh học 11 kết nối tri thức
Giải chuyên đề kinh tế pháp luật 11 kết nối tri thức
Giải chuyên đề lịch sử 11 kết nối tri thức
Giải chuyên đề địa lí 11 kết nối tri thức
Giải chuyên đề mĩ thuật 11 kết nối tri thức
Giải chuyên đề âm nhạc 11 kết nối tri thức
Giải chuyên đề công nghệ chăn nuôi 11 kết nối tri thức
Giải chuyên đề công nghệ cơ khí 11 kết nối tri thức
Giải chuyên đề tin học 11 định hướng Khoa học máy tính kết nối tri thức
Giải chuyên đề tin học 11 định hướng Tin học ứng dụng kết nối tri thức
Giải chuyên đề quốc phòng an ninh 11 kết nối tri thức
Giải chuyên đề hoạt động trải nghiệm hướng nghiệp 11 kết nối tri thức
Giải chuyên đề học tập lớp 11 chân trời sáng tạo
Giải chuyên đề học tập lớp 11 cánh diều
Trắc nghiệm 11 Kết nối tri thức
Trắc nghiệm 11 Chân trời sáng tạo
Trắc nghiệm 11 Cánh diều
Bộ đề thi, đề kiểm tra lớp 11 kết nối tri thức
Đề thi Toán 11 Kết nối tri thức
Đề thi ngữ văn 11 Kết nối tri thức
Đề thi vật lí 11 Kết nối tri thức
Đề thi sinh học 11 Kết nối tri thức
Đề thi hóa học 11 Kết nối tri thức
Đề thi lịch sử 11 Kết nối tri thức
Đề thi địa lí 11 Kết nối tri thức
Đề thi kinh tế pháp luật 11 Kết nối tri thức
Đề thi công nghệ cơ khí 11 Kết nối tri thức
Đề thi công nghệ chăn nuôi 11 Kết nối tri thức
Đề thi tin học ứng dụng 11 Kết nối tri thức
Đề thi khoa học máy tính 11 Kết nối tri thức
Bộ đề thi, đề kiểm tra lớp 11 chân trời sáng tạo
Bộ đề thi, đề kiểm tra lớp 11 cánh diều
Đề thi Toán 11 Cánh diều
Đề thi ngữ văn 11 Cánh diều
Đề thi vật lí 11 Cánh diều
Đề thi sinh học 11 Cánh diều
Đề thi hóa học 11 Cánh diều
Đề thi lịch sử 11 Cánh diều
Đề thi địa lí 11 Cánh diều
Đề thi kinh tế pháp luật 11 Cánh diều
Đề thi công nghệ cơ khí 11 Cánh diều
Đề thi công nghệ chăn nuôi 11 Cánh diều
Đề thi tin học ứng dụng 11 Cánh diều
Đề thi khoa học máy tính 11 Cánh diều




Bình luận