BÀI 3. HÀM SỐ MŨ. HÀM SỐ LÔGARIT

I. Hàm số mũ

Bài 1: Xét bài toán ở phần mở đầu.

a) Tính số tiền doanh nghiệp đó có được sau 1 năm, 2 năm, 3 năm

b) Dự đoán công thức tính số tiền doanh nghiệp đó có được sau n năm

Đáp án: 

a) Số tiền doanh nghiệp đó có được:

+ Sau 1 năm: 1 000 000 000+1 000 000 000 . 6,2%=1 062 000 000 (đồng)

+ Sau 2 năm: 1 062 000 000+1 062 000 000 . 6,2%=1 127 844 000 (đồng)

+ Sau 3 năm: 1 127 844 000+1 127 844 000 . 6,2%=1 197 770 328 (đồng)

b) Dự đoán công thức tính số tiền doanh nghiệp có được sau n năm là:

A=1 000 000 000 . (1+6,2%)$^{n}$

Bài 2: Cho hai ví dụ về hàm số mũ 

Đáp án: 

y=0,5$^{x}$ 

y=(3$\sqrt{3}$)$^{x}$ 

Bài 3: Cho hàm số mũ y=2$^{x}$...

Đáp án: 

a) y=2$^{x}$

b) Ta biểu diễn các điểm của câu a

c) Tọa độ giao điểm của đồ thị y=2$^{x}$ với trục tung là 0;1 

Đồ thị không cắt trục hoành.

d) • 2$^{x}$ =+∞ ;  2$^{x}$ =0

• Hàm số y=2$^{x}$ đồng biến trên R.

Bài 4: Cho hàm số mũ y=($\frac{1}{2}$)$^{x}$...

Đáp án: 

a) y=($\frac{1}{2}$)$^{x}$

b) Ta biểu diễn các điểm ở câu a

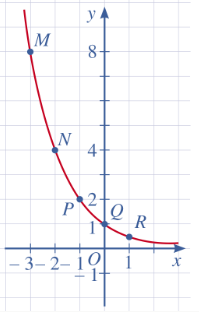
c) Tọa độ giao điểm của đồ thị hàm số y=($\frac{1}{2}$)$^{x}$ với trục tung là 0;1

Đồ thị hàm số y=($\frac{1}{2}$)$^{x}$ không cắt trục hoành.

d) ($\frac{1}{2}$)$^{x}$ =0 ; ($\frac{1}{2}$)$^{x}$ =+∞

Hàm số y=($\frac{1}{2}$)$^{x}$ nghịch biến trên R.

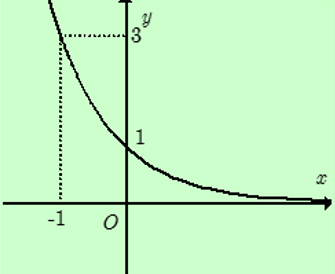
Bài 5: Lập bảng biến thiên và vẽ đồ thị hàm số y=($\frac{1}{3}$)$^{x}$

Đáp án: 

- Hàm số y=($\frac{1}{3}$)$^{x}$ là hàm số nghịch biến trên R.

- Vì hàm số y=($\frac{1}{3}$)$^{x}$ có cơ số 0<$\frac{1}{3}$<1 nên ta có bảng biến thiên sau:

Đồ thị hàm số y=($\frac{1}{3}$)$^{x}$ đi qua các điểm A(-1;3); B(0;1); C(1;$\frac{1}{9}$); D(2;$\frac{1}{9}$); E(3;$\frac{1}{27}$)

II. Hàm số lôgarit

Bài 1: Tìm giá trị y tương ứng với giá trị của x trong bảng sau: 

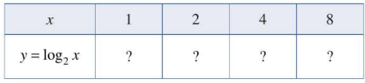
Đáp án: 

Bài 2: Cho hai ví dụ về hàm số lôgarit 

Đáp án: 

x    

(x-1)

Bài 3: Cho hàm số lôgarit y=x ...

Đáp án: 

a) y=x

b) Biểu diễn các điểm ở câu a ta được

c) Tọa độ giao điểm của đồ thị hàm số y=x với trục hoành là 1;0

Đồ thị hàm số không cắt trục tung.

d) (x) =0; (x) =+∞

Hàm số y=x đồng biến trên (0; +∞).

Bài 4: Cho hàm số lôgarit y=x ...

Đáp án: 

a) 

b) Biểu diễn các điểm ở câu a, ta được:

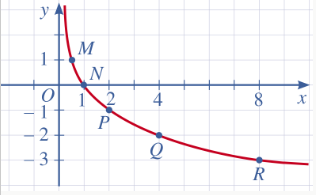
c) Tọa độ giao điểm của đồ thị hàm số y=x với trục hoành là 1;0

+ Đồ thị hàm số không cắt trục tung.

d) (x) =0 ; (x) =-∞

Hàm số y=x nghịch biến trên 0;+∞.

Bài 5: Lập bảng biến thiên và vẽ đồ thị hàm số y=x

Đáp án: 

Ta được bảng biến thiên:

+ Ta có bảng sau

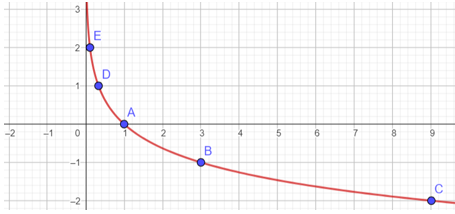
=> Đồ thị của hàm số y=x là một đường cong liền nét đi qua các điểm A(1;0); B(3; -1); C(9;-2);D($\frac{1}{3}$;1); E($\frac{1}{9}$;2)

III. Bài tập

Bài 1: Tìm tập xác định của các hàm số…

Đáp án: 

a) D=R

b) D=($\frac{3}{2}$;+∞)

c) D=(-2;2)

Bài 2: Trong các hàm số sau, hàm số nào đồng biến, hàm số nào nghịch biến trên khoảng xác định của hàm số đó? Vì sao?...

Đáp án: 

a) Hàm số y=($\frac{\sqrt{3}}{2}$)$^{x}$ nghịch biến trên R. Vì 0<$\frac{\sqrt{3}}{2}$<1

b) Hàm số y=($\frac{\sqrt[3]{26}}{2}$)$^{x}$ nghịch biến trên R. Vì 0<$\frac{\sqrt[3]{26}}{2}$<1

c) Hàm số y=log$_{\pi }$x đồng biến trên (0;+∞). Vì π>1

d) Hàm số y=log$_{\frac{\sqrt{15}}{4}}$4 x nghịch biến trên (0;+∞). Vì 0<$\frac{\sqrt{15}}{4}$<1

Bài 3: Lập bảng biến thiên và vẽ đồ thị hàm số…

Đáp án: 

a) y=4$^{x}$

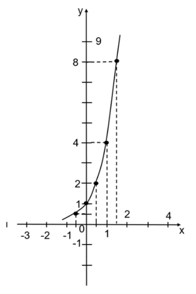
Đồ thị hàm số y=4$^{x}$ là đường cong đi qua A(-$\frac{1}{2}$;$\frac{1}{2}$), B(0;1), C(1;4), D($\frac{1}{2}$;2), E($\frac{3}{2}$;8)

b) y=log$_{\frac{\sqrt{1}}{4}}$x

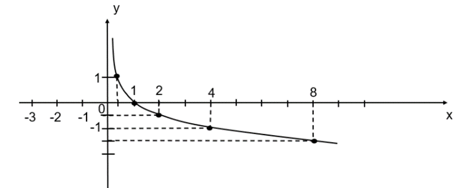
Đồ thị hàm số y=log$_{\frac{\sqrt{1}}{4}}$x là đường cong đi qua A($\frac{1}{4}$;1), B(1;0), C(2;-$\frac{1}{2}$), D(4;-1), E(8;-$\frac{3}{2}$)

Bài 4: Ta coi năm lấy làm mốc để tính dân số của một vùng (hoặc một quốc gia) là năm 0…

Đáp án: 

Dân số năm 2030 của Việt nam là:

S=A.e$^{rt}$=98 564 407 . e$^{0,93$^{o}$/$_{o}$.0}$≈107 169 341 người.

Bài 5: Các nhà tâm lí học sử dụng mô hình hàm số mũ để mô phỏng quá trình học tập của một học sinh như sau:…

Đáp án: 

Trong 2 ngày, em học sinh nhớ được:

f(2)=25 . 1-e$^{-0,2.2}$≈8 (đơn vị kiến thức)

Trong 2 ngày, em học sinh nhớ được:

f(8)=25 . 1-e$^{-0,2.8}$≈20 (đơn vị kiến thức)

Bài 6: Chỉ số hay độ pH của một dung dịch được tính theo công thức:…

Đáp án: 

Mẫu 1: 

 pH=-log [8.10$^{-7}$] =-(log 8 +log 10$^{-7}$)  =7-3log 2  

Mẫu 2: pH=-log [2.10$^{-9}$] =-(log 2 +log 10$^{-9}$ )=9-log 2

Nhận thấy 7-3log 2 <9-log 2 nên độ pH của mẫu 2 lớn hơn của mẫu 1

Bài 7: Một người gửi 10 triệu đồng vào ngân hàng theo hình thức lãi kép có kì hạn là 12 tháng với lãi suất 6%/ năm…

Đáp án: 

Số năm để có được tổng cả vốn và lãi 15 triệu đồng là:

y=($\frac{15}{10}$) ≈7 (năm)

Số năm để có được tổng cả vốn và lãi 20 triệu đồng là:

y=($\frac{20}{10}$) ≈12 (năm)