BÀI 3. GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG. GÓC NHỊ DIỆN

I. Định nghĩa

Bài 1: Quan sát Hình 32 và cho biết… 

Đáp án: 

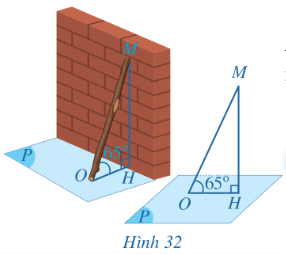
a) Ta có: MH⊥(P), O∈(P) => Hình chiếu của MO trên (P) là HO.

b) Góc giữa MO và hình chiếu của đường thẳng đó trên (P) là $\widehat{MOH}$.

Bài 2: Giả sử ở những giây đầu tiên sau khi cất cánh. máy bay chuyển động theo một đường thẳng tạo với mặt đất một góc 20$^{\circ}$ và có vận tốc 200 km/h. Tính độ cao của máy bay so với mặt đất theo đơn vị mét sau khi máy bay rời khỏi mặt đất 2 giây (làm tròn kết quả đến hàng phần mười). 

Đáp án: 

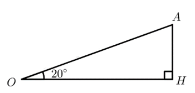
Đổi 200km/h =$\frac{500}{9}$ m/s

OA là quãng đường máy bay bay sau 2 giây, OH là độ cao của máy bay so với mặt đất, AOH là chỉ số đo góc giữa đường thẳng máy bay và mặt đất.

Quãng đường máy bay bay được sau 2 giây là:

$\frac{500}{9}$ . 2=$\frac{1000}{9}$ (m)

∆OAH vuông tại H nên ta có:

AH=OA.sin $\widehat{AOH}$ =$\frac{1000}{9}$.sin 20$^{\circ}$ ≈38 (m)

II. Góc nhị diện

Bài 1: Quan sát hình ảnh một quyển số được mở ra…

Đáp án: 

Hai nửa mặt phẳng có chung bờ

Bài 2: Trong không gian cho hai mặt phẳng $\alpha $,$\beta $ …

Đáp án: 

Hai mặt phẳng $\alpha $ và $\beta $ tạo nên 4 góc nhị diện có cạnh của góc nhị diện là đường thẳng d.

Bài 3: Cho góc nhị diện có hai mặt là hai nửa mặt phẳng (P), (Q) và cạnh của góc nhị diện là đường thẳng d…

Đáp án: 

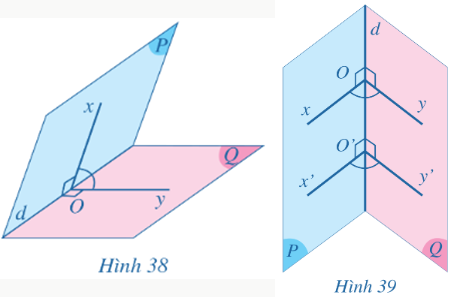
Trong P: $\left\{\begin{matrix}Ox\perp d & \\ O'x'\perp d & \end{matrix}\right.$ => Ox//O'x'

Trong (Q): $\left\{\begin{matrix}Oy\perp d & \\ O'y'\perp d & \end{matrix}\right.$ => Oy//O'y'

Vậy $\widehat{xOy}$=$\widehat{x'Oy'}$.

Bài 4: Cho hình chóp S.ABCD có đáy ABCD là hình vuông…

Đáp án: 

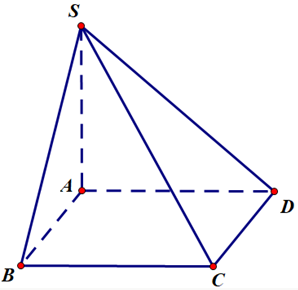
a. Ta có: AB⊥SA, AD⊥SA (Do SA⊥(ABCD))

Nên góc nhị diện [B,SA,D] là góc $\widehat{BAD}$=90$^{\circ}$ (ABCD là hình vuông)

b. Vì AB⊥SA, AC⊥SA (Do SA⊥(ABCD))

Nên góc nhị diện [B,SA,C] là góc $\widehat{BAC}$=45$^{\circ}$ (ABCD là hình vuông)

III. Bài tập

Bài 1: S.ABCD có SA ⊥ (ABCD)…

Đáp án: 

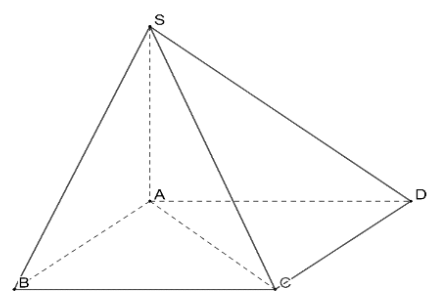
a) Ta có AB⊥SA, AC⊥SA (Do SA⊥(ABCD))

Nên góc nhị diện [B,SA,C]=$\widehat{BAC}$

Mà ∆ABC đều cạnh a => [B,SA,C]=$\widehat{BAC}$=60$^{\circ}$

b) Ta có AB⊥SA, AD⊥SA (Do SA⊥(ABCD))

Nên góc nhị diện [B,SA,D]=$\widehat{BAD}$

Mà ∆ACD đều cạnh a => $\widehat{CAD}$=60$^{\circ}$

=> [B,SA,D]=$\widehat{BAD}$=$\widehat{BAC}$+$\widehat{CAD}$=120$^{\circ}$

c) Do SA⊥(ABCD) nên AC là hình chiếu của SC trên (ABCD)

=> (SC, (ABCD)) = $\widehat{SCA}$

Mà ∆SAC vuông cân tại A => $\widehat{SCA}$=45$^{\circ}$

Bài 2: Cho hình chóp S.ABCD có đáy ABCD là hình vuông…

Đáp án: 

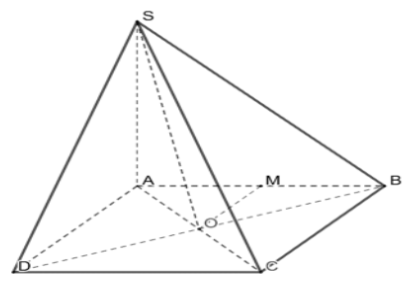
a) Do SO⊥(ABCD) => (SA, ABCD) = $\widehat{SAC}$

Mà ∆SAC đều => $\widehat{SAC}$=60$^{\circ}$

b) Do SO⊥(ABCD)⇒AO⊥AC;  AC⊥BD (ABCD là hình vuông)

=> AC⊥($\widehat{ABD}$)

⇒ (SA, ($\widehat{SBD}$))=(SA,SO)=$\widehat{ASO}$=$\frac{1}{2} \widehat{ASC}$=30$^{\circ}$

c) Ta có OM⊥SO;OD⊥SO (SO⊥(ABCD))

[M,SO,D]=$\widehat{MOD}$=$\widehat{MOA}$+$\widehat{AOD}$ 

Mà $\widehat{AOD}$=90$^{\circ}$ (ABCD là hình vuông)

∆OAB vuông cân tại O; OM là đường trung tuyến trong ∆OAB

=> OM là đường phân giác của $\widehat{AOB}$ 

=> $\widehat{MOA}$=45$^{\circ}$

=> [M,SO,D]=$\widehat{MOD}$=$\widehat{MOA}$+$\widehat{AOD}$

=45$^{\circ}$+90$^{\circ}$=135$^{\circ}$

Bài 3: Dốc là đoạn đường thẳng nối hai khu vực hay hai vùng có độ cao khác nhau…

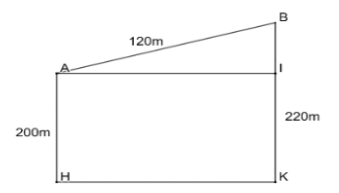
Đáp án: 

AB là chiều dài con dốc, AH là độ cao của điểm A so với mặt nước biển, BK là độ cao của điểm B so với mặt nước biển, BI là chiều cao của con dốc, BAI chỉ độ dốc.

Xét hình chữ nhật AHKB, ta có:

=> IK=AH=200⇒BI=BK-IK=20

Xét ∆ABI vuông tại I, ta có:

=> sin $\widehat{ABI}$=$\frac{BI}{AB}$=$\frac{20}{120}$=$\frac{1}{6}$ 

=> $\widehat{ABI} \approx $9,590 hay 10,66%

Vậy độ dốc của con dốc đó là 10,66%

Bài 4: Trong Hình 42, máy tính xách tay đang mở gợi nên hình ảnh của một góc nhị diện…

Đáp án: 

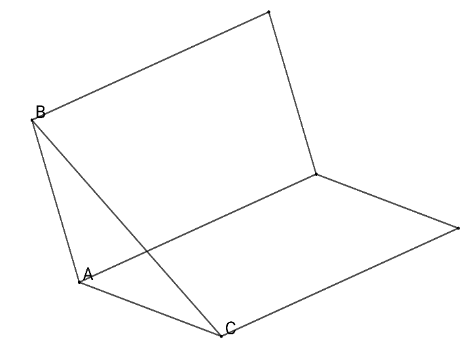
CAB là góc phẳng nhị diện của góc nhị diện cần tính. 

Xét ∆ABC, ta có: 

cos$\widehat{CAB}$=$\frac{AB^{2}+AC^{2}-BC^{2}}{2.AB.AC}$=$\frac{30^{2}+30^{2}-(30\sqrt{3})^{2}}{2.30.30}$=-$\frac{1}{2}$ ⇒$\widehat{CAB}$=120$^{\circ}$

Bài 5: Trong Hình 43, xét các góc nhị diện có góc phẳng nhị diện tương ứng…

Đáp án: 

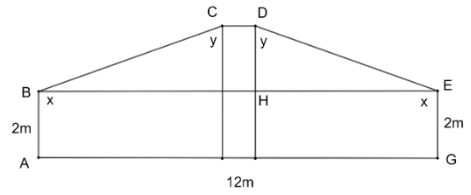
Kẻ DH⊥AG và cắt BE tại H; 

Xét ∆DHE vuông tại H và DH=2m;HE=5,5m

=> tan $\widehat{HED}$ =$\frac{DH}{HE}$=$\frac{2}{5,5}$

=> $\widehat{HED} \approx $20$^{\circ}$=> $\widehat{EDH} \approx $70$^{\circ}$

Ta có:

+) x=$\widehat{HEG}$+$\widehat{HED}$=90$^{\circ}$+20$^{\circ}$=110$^{\circ}$

+) y=$\widehat{CDH}$+$\widehat{EDH}$=90$^{\circ}$+70$^{\circ}$=160$^{\circ}$

Bài 6: Cho hình chóp S.ABC có SA ⊥ (ABC)… 

Đáp án: 

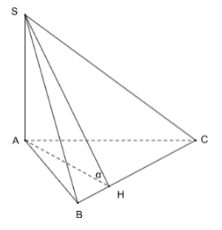
Kẻ đường cao AH => AH⊥BC

Ta có:  SA$\perp $(ABC) =>BC⊥SA⇒BC⊥(SAH)⇒BC⊥SH 

Vậy [A, BC, S] = $\widehat{AHS}$=α

Xét ∆SAH vuông tại A ta có:

=>  cos α =$\frac{AH}{SH}$. Mặt khác $\frac{S_{ABC}}{S_{SBC}}$=$\frac{\frac{1}{2}AH.BC}{\frac{1}{2}SH.BC}$=$\frac{AH}{SH}$

=> cos α=$\frac{S_{ABC}}{S_{SBC}}$