BÀI 2. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG

I. Định nghĩa

Bài 1: Hình 10 mô tả một người thợ xây đang thả dây dọi vuông góc với nền nhà…

Đáp án: 

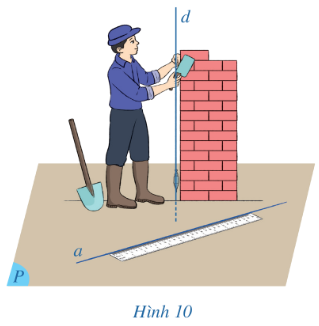
Đường thẳng d $\perp $ đường thẳng a.

II. Điều kiện để đường thẳng vuông góc với mặt phẳng

Bài 1: Hình 12 mô tả cửa tròn xoay, ở đó trục cửa và hai mép cửa gợi nên hình ảnh các đường thẳng d, a, b; sàn nhà coi như mặt phẳng (P) chứa a và b. Hỏi đường thẳng d có vuông góc với mặt phẳng (P) hay không? 

Đáp án: 

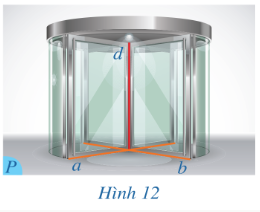
Vì d⊥a; d⊥b;  a ∩ b. Vậy d⊥(P)

Bài 2: Cho hình chóp S.ABCD có đáy ABCD là hình thoi, SA ⊥ (ABCD) Chứng minh rằng BD ⊥ (SAC) 

Đáp án: 

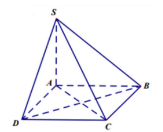
Ta có:

+) SA⊥(ABCD) => SA⊥BD

+) ABCD là hình thoi => AC⊥BD

Xét mp(SAC) có: SA∩AC=A

SA⊥BD, AC⊥BD (cmt) => BD⊥(SAC).

III. Tính chất

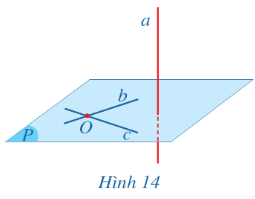
Bài 1: Cho điểm O và đường thẳng a…

Đáp án: 

a) Ta có:

$\left\{\begin{matrix}a\perp b\subset (P) & \\ a\perp c\subset (P) & \\ b\cap c & \end{matrix}\right.$ => a⊥(P)

b) Chỉ có 1 mặt phẳng duy nhất vuông góc với a và đi qua điểm O .

Bài 2: Hình 17 mô tả một cửa gỗ có dạng hình chữ nhật…

Đáp án: 

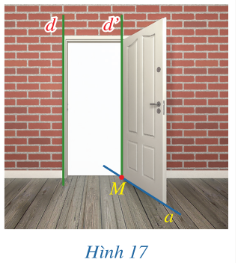
Do sàn nhà là một mặt phẳng luôn vuông góc với đường thẳng d. Mà đường thẳng a lại thuộc mặt phẳng đó nên đường thẳng d luôn vuông góc với đường thẳng a. 

Bài 3: Cho mặt phẳng (P) và điểm O. Gọi a, b là hai đường thẳng cắt nhau thuộc mặt phẳng (P) sao cho a và b không đi qua O. Lấy hai mặt phẳng (Q), (R) lần lượt đi qua O và vuông góc a, b (Hình 18). 

Đáp án: 

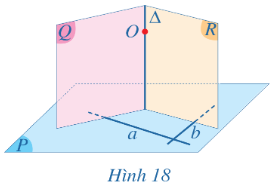
a) Ta có:

$\left\{\begin{matrix}a\perp (Q) & \\ \Delta \subset (Q) & \end{matrix}\right.$ => a⊥∆

Lại có:

$\left\{\begin{matrix}b\perp (R) & \\ \Delta \subset (R) & \end{matrix}\right.$ => b⊥∆

Vì

$\left\{\begin{matrix}\Delta \perp a\subset (P) & \\ \Delta \perp b\subset (P) & \\ a\cap b & \end{matrix}\right.$ => ∆⊥P

b) Chỉ có duy nhất 1 đường thẳng vuông góc với (P) và đi qua O

Bài 4: Cho mặt phẳng (P) và đường thẳng a cắt nhau tại điểm O, a ⊥ (P). Giả sử điểm M thỏa mãn OM ⊥ (P) Chứng minh rằng M ∈ a 

Đáp án: 

Vì chỉ có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước nên:

$\left\{\begin{matrix}a\cap (P)=O & \\ a\perp (P) & \\ OM\perp (P) & \end{matrix}\right.$ => M∈a

IV. Liên hệ giữa quan hệ song song và quan hệ vuông góc của đường thẳng và mặt phẳng.

Bài 1: Trong Hình 19, hai thanh sắt và bản phẳng để ngồi…

Đáp án: 

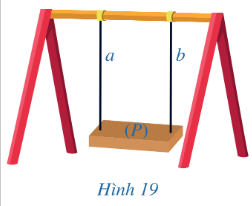
a) Nếu a // b và (P) a thì (P) b 

b) Nếu a và b cùng vuông góc với (P) thì a // b

Bài 2: Cho đường thẳng d và mặt phẳng (P) cắt nhau tại điểm O…

Đáp án: 

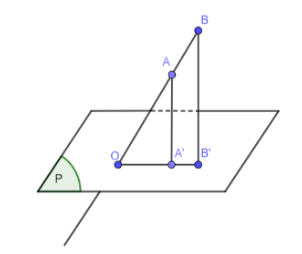
Do AA'$\perp $(P), BB'$\perp $(P) => AA'//BB'

Xét ∆OBB' có:

AA'//BB' => $\frac{AA'}{BB'}$=$\frac{OA}{OB}$ (định lí Thalès).

Bài 3: Trong Hình 21, hai mặt sàn của nhà cao tầng và cột trụ bê tông gợi nên hình ảnh hai mặt phẳng (P), (Q) phân biệt và đường thẳng a…

Đáp án: 

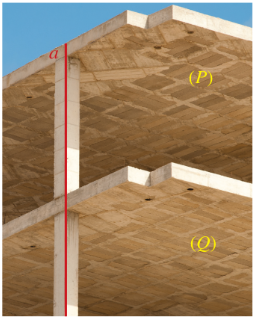
a) Nếu (P)//(Q) và a⊥(P) => a⊥(Q)

b) Nếu (P)⊥a và (Q)⊥a => (P)//(Q)

Bài 4: Cho hình chóp S.ABC có SA ⊥ (ABC)…

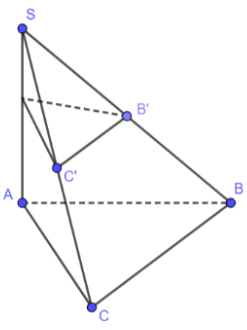
Đáp án: 

Ta có:

$\left\{\begin{matrix}(P)\perp SA & \\ (ABC)\perp SA & \end{matrix}\right.$  => (P)//(ABC)

Vậy B'C'//BC.

V. Phép chiếu vuông góc

Bài 1: Trong mặt phẳng (P). Xét một điểm M tùy ý trong không gian.

a) Có bao nhiêu đường thẳng d đi qua điểm M và vuông góc với mặt phẳng (P)?

b) Đường thẳng d cắt mặt phẳng (P) tại bao nhiêu giao điểm

Đáp án: 

a) Có 1 đường thẳng d đi qua M và vuông góc với (P)

b) Đường thẳng (d) cắt (P) tại 1 điểm

Gọi M' = d ∩ (P) (Hình 24). M' được gọi là hình chiếu vuông góc của M lên P.

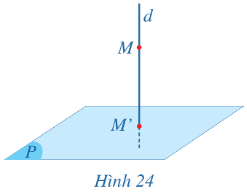
Bài 2: Cho mặt phẳng (P) và đoạn thẳng AB. Xác định hình chiếu của đoạn thẳng AB trên mặt phẳng (P) 

Đáp án: 

Trường hợp 1: AB⊄(P):

- Bước 1: Tìm hình chiếu A' của A lên (P)

- Bước 2: Tìm hình chiếu B' của B lên (P)

- Bước 3: Nối A' với B' ta được đoạn thẳng A'B' là hình chiếu của AB lên (P).

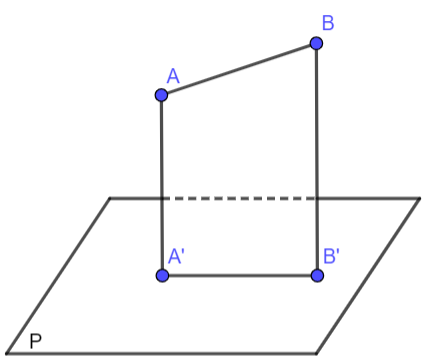
Trường hợp 2: Đoạn AB có A hoặc B thuộc (P).

- Bước 1: Hình chiếu của điểm A (hoặc B) thuộc (P) lên (P) là chính nó.

- Bước 2: Xác định hình chiếu A' (hoặc B’) của điểm còn lại lên (P)

- Bước 3: Nối điểm A và B' (hoặc A' và B) ta được hình chiếu của đoạn AB lên (P).

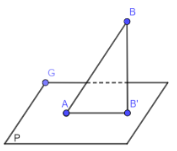
Trường hợp 3: AB⊥(P) tại A (hoặc B).

- Sử dụng kết quả của Ví dụ 8, ta có:

- Hình chiếu của AB lên (P) chính là điểm B (hoặc điểm A)

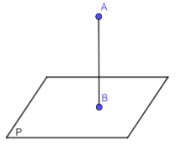
Trường hợp 4: AB⊂(P)

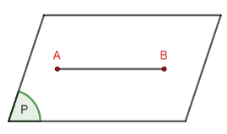
VI. Định lí ba đường vuông góc

Bài 1: Trong Hình 27, mặt sàn gợi nên hình ảnh mặt phẳng (P), đường thẳng a không vuông góc với mặt phẳng (P)…

Đáp án: 

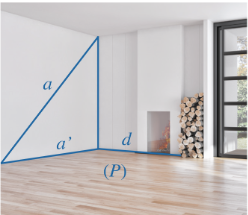
Gọi A, B là 2 điểm phân biệt thuộc a

Gọi A’, B’ lần lượt là hình chiếu của A và B trên (P)

a) Do d ⊂ (P) => d ⊥ AA′

Vậy nếu d ⊥ a′ thì d ⊥ (a,a′) => d ⊥ a

b) Ngược lại, nếu d ⊥ a thì d ⊥  (a,a′) => d ⊥ a′

Bài 2: Cho hình chóp S.ABCD có SA ⊥ (ABCD) và đáy ABCD là hình chữ nhật. Chứng minh rằng các tam giác SBC và SCD là các tam giác vuông.

Đáp án: 

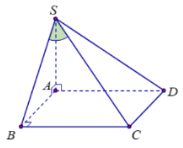
Ta có: BC ⊥ AB (ABCD là hình chữ nhật)

BC⊥ SA (SA ⊥ (ABCD) 

⇒ BC ⊥ (SAB) ⇒ BC ⊥ SB

=> ∆SBC vuông tại B

 Có CD ⊥ AD (ABCD là hình chữ nhật)

       CD ⊥ SA (vì (SA ⊥ (ABCD)) 

=> CD ⊥ (SAD) ⇒ CD ⊥ SD

=> ∆SCD vuông tại D

VII. Bài tập

Bài 1: Quan sát Hình 30 (hai cột của biển báo, mặt đường), cho biết hình đó gợi nên tính chất nào về quan hệ vuông góc giữa đường thẳng và mặt phẳng. 

Đáp án: 

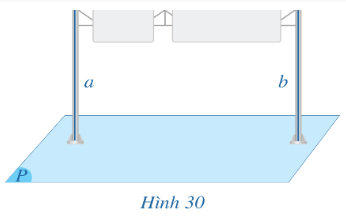
Gọi nên các tính chất là:

• Cho hai đường thẳng song song. Một mặt phẳng vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.

• Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.

Bài 2: Cho hình chóp S.ABC. Gọi H là hình chiếu của S trên mặt phẳng (ABC)…

Đáp án: 

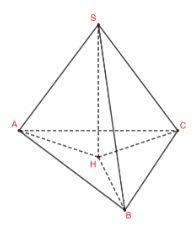
a) +) H là hình chiếu của S trên (ABC); A là hình chiếu của A trên (ABC)

⇒ HA là hình chiếu của SA trên (ABC)

+) B là hình chiếu của B trên (ABC)

⇒ HB là hình chiếu của SB trên (ABC)

+) C là hình chiếu của C trên (ABC)

⇒ HC là hình chiếu của SC trên (ABC)

b) H là hình chiếu của S lên mp(ABC) => SH⊥(ABC) 

=> SH⊥AB;SH⊥AC;SH⊥BC

Ta có:

$\left\{\begin{matrix}SA\perp BC & \\ SH\perp BC & \\ SA\perp SH & \\ SA,SH\subset (SAH) & \end{matrix}\right.$ => BC⊥(SAH) => BC⊥AH 

Tương tự:

$\left\{\begin{matrix}SC\perp AB & \\ SH\perp AB & \\ SC\cap SH=S & \\ SC,SH\subset (SCH) & \end{matrix}\right.$=> AB⊥(SC) => AB⊥CH 

=> H là trực tâm ∆ABC

=> CH⊥AB, mà SH⊥AB => AB⊥(SCH)

=> AB⊥SC.

Bài 3: Cho tứ diện ABCD có AB ⊥ (BCD)…

Đáp án: 

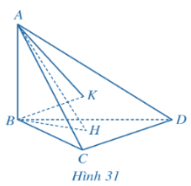
a) Ta có: AB⊥(BCD) => AB⊥CD 

Mà H là trực tâm ∆BCD => BH⊥CD 

=> CD⊥(ABH)

b) Ta có: AB$\perp $(BCD) => AB⊥CD 

Mà K là trực tâm ∆ACD => AK⊥CD

=> CD⊥(ABK)

c) Theo a và b: CD⊥(ABH),CD⊥(ABK). Nên (ABH)≡(ABK)

Gọi BH cắt CD tại I. Xét BCD, ta có: 

AI⊥CD tại I (Vì AI∈(ABH), (ABH)⊥CD).

Mà AK  ⊥CD và AI, AK∈(ACD) ⇒A, K, I thẳng hàng.

Vậy AK, BH, CD cùng đi qua một điểm.

Bài 4: Cho tứ diện ABCD có đáy là hình bình hành… 

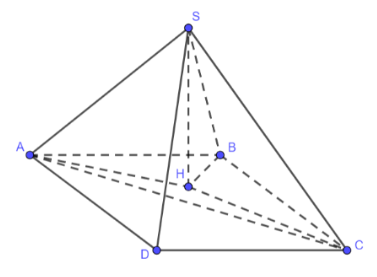
Đáp án: 

a) Có SH⊥(ABCD) (gt) => SH⊥(ABC) => SH⊥BC 

Mà AH⊥BC (H là trực tâm ∆ABC) 

=> BC⊥(SAH) => SA⊥BC

Lại có: BC//AD (ABCD là hình bình hành) => SA⊥AD

b) Có SH$\perp $(ABCD) (gt) => SH$\perp $(ABC) => SHAB 

Mà CH⊥AB (H là trực tâm ∆ABC) 

=> AB⊥(SHC) => AB⊥SC

Lại có AB//CD (ABCD là hình bình hành) => SC⊥CD

Bài 5: Cho hình chóp S.ABCD có SA ⊥ (ABC), BC ⊥ AB…

Đáp án: 

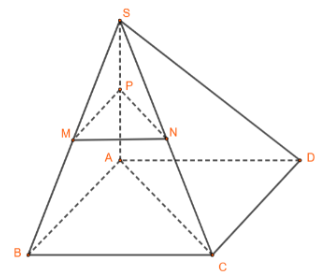
Có SA⊥(ABC) => SA⊥BC; mà BC ⊥ AB

=> BC ⊥ (SAB) => BC ⊥ MP 

Xét △SBC có M, N lần lượt là trung điểm của SB, SC

=> MN là đường trung bình của ∆SBC => MN // BC

=> MN ⊥ MP =>  ∆MNP vuông tại M