I. BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

HĐ1: 

Điều kiện ràng buộc đối với x và y là:

0,06x + 0,05y ≤ 500

Kết luận:

- Bất phương trình bậc nhất hai ẩn x, y là bất phương trình có một trong các dạng sau: ax + by < c; ax + by > c; ax + by ≤ c; ax + by ≥ c, trong đó: a, b, c là những số thực cho trước với a, b không đồng thời bằng 0; x và y là các ẩn.

- Cho bất phương trình bậc nhất hai ẩn ax + by < c (*)

Mỗi cặp số $(x_o; y_o)$ sao cho $ax_o + by_o < c$ được gọi là một nghiệm của bất phương trình (*).

Trong mặt phẳng tọa độ Oxy, tập hợp các điểm có tọa độ là nghiệm của bất phương trình (*) được gọi là miền nghiệm của bất phương trình đó.

Ví dụ 1 (SGK - tr21)

Luyện tập 1:

a) 5x + 3y < 20 là bất phương trình bậc nhất hai ẩn.

Chọn x = 1; y = 1, ta có: 5.1 + 3.1 = 8 < 20 là mệnh đề đúng.

Vậy (1; 1) là nghiệm của bất phương trình.

b) $3x - \frac{5}{y}$ > 2 không phải là bất phương trình bậc nhất hai ẩn vì có ẩn y ở mẫu.

II. BIỂU DIỄN MIỀN NGHIỆM CỦA BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Mô tả miền nghiệm của bất phương trình bậc nhất hai ẩn

HĐ2: (SGK - tr21,22)

HĐ3: Cho bất phương trình $2x - y > 2$ (3) 

a) Đường thẳng d: $y = 2x – 2$

Đường thẳng d đi qua hai điểm (0; – 2) và (1; 0). Ta vẽ đường thẳng d như sau: 

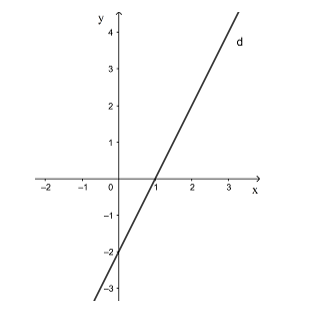
b) Xét điểm M(2; – 1)

Thay x = 2 và y = – 1 vào bất phương trình (3) ta được: 2 . 2 – (– 1) > 2 ⇔ 5 > 2 (luôn đúng). 

Vậy (2; – 1) là nghiệm của bất phương trình (3). 

c) Đường thẳng d chia mặt phẳng tọa độ thành hai nửa mặt phẳng. Gạch đi nửa mặt phẳng không chứa điểm M(2; -1), ta có:

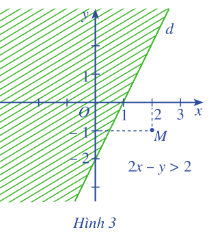
Kết luận:

Trong mặt phẳng tọa độ Oxy, đường thẳng d: ax + by = c chia mặt phẳng thành hai nửa mặt phẳng. Một trong hai nửa mặt phẳng (không kể đường thẳng d) là miền nghiệm của bất phương trình ax + by < c, nửa mặt phẳng còn lại (không kể đường thẳng d) là miền nghiệm của bất phương trình ax + by > c.

Chú ý: Đối với bất phương trình dạng ax + by ≤ c hoặc ax + by ≥ c thì miền nghiệm là một trong hai nửa mặt phẳng kể cả đường thẳng d.

Ví dụ 2 (SGK - tr23)

Biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn

Các bước biểu diễn miền nghiệm của bất phương trình ax + by < c trong mặt phẳng tọa độ Oxy như sau:

- Bước 1: Vẽ đường thẳng d: ax + by = c. Đường thẳng d chia mặt phẳng tọa độ thành hai nửa mặt phẳng.

- Bước 2: Lấy một điểm $M(x_o; y_o)$ không nằm trên d (ta thường lấy gốc tọa độ O nếu c ≠ 0). Tính $ax_o + by_o$ và so sánh với c.

- Bước 3: Kết luận

+ Nếu $ax_o + by_o < c$ thì nửa mặt phẳng (không kể đường thẳng d) chứa điểm M là miền nghiệm của bất phương trình ax + by < c.

+ Nếu $ax_o + by_o > c$ thì nửa mặt phẳng (không kể đường thẳng d) không chứa điểm M là miền nghiệm của bất phương trình ax + by < c.

Ví dụ 3 (SGK - tr23)

Luyện tập 2:

a) x - 2y < 4

+ Vẽ đường thẳng d: x – 2y = 4

Cho x = 0 thì y = – 2, cho y = 0 thì x = 4. Đường thẳng d đi qua 2 điểm (0; – 2) và (4; 0). 

+ Lấy điểm O (0; 0). Ta có: 0 – 0 = 0 < 4.

Vậy miền nghiệm của bất phương trình x – 2y < 4 là nửa mặt phẳng không bị gạch chứa điểm O (0; 0) không kể đường thẳng d. 

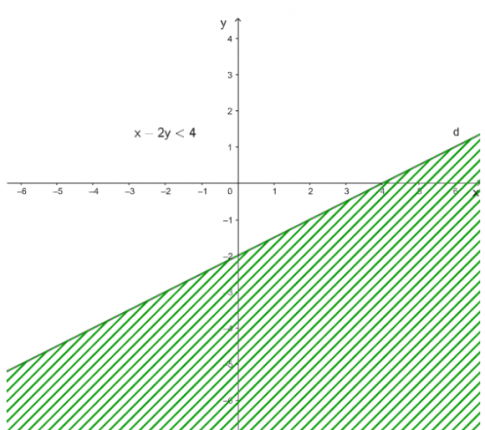
b) x + 3y ≥ 6

+ Vẽ đường thẳng d: x + 3y = 6

Cho x = 0 thì y = 2, cho y = 0 thì x = 6, do đó đường thẳng d đi qua hai điểm (0; 2) và (6; 0). 

+ Lấy điểm O (0; 0). Ta có: 0 + 3.0 = 0 < 6. 

Vậy miền nghiệm của bất phương trình x + 3y ≥ 6 là nửa mặt phẳng không bị gạch không chứa điểm O (0; 0) kể cả đường thẳng d. 

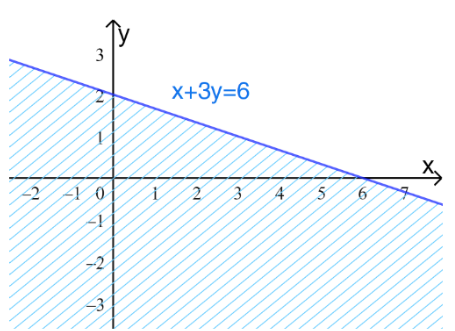
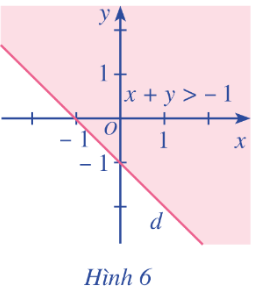
Chú ý: Thông thường khi sử dụng phần mềm toán học để biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn, miền nghiệm của bất phương trình đó được tô màu. 

Chẳng hạn, miền nghiệm của bất phương trình x + y > -1 đươc tô như Hình 6.