1. HAI MẶT PHẲNG SONG SONG

Bài 1: Hộp giấy có các mặt là hình vuông...

Đáp án: 

a) Có ba điểm chung không thẳng hàng: (ABC) và (ABD); (AA'B) và (ABB'); (BB'C) và (BCC');...

b) Không có cặp nào

c) Các cặp không có điểm chung: (ABCD) và (A'B'C'D'); (ADD'A') và (BCC'B'); (ABB'A') và (DCC'D')

Bài 2: Tìm một số mặt phẳng song song có trong hình chụp...

Đáp án: 

Các mặt phẳng song song có trong bức hình là: Bìa của cuốn sách, các tấm ngăn đứng, các tấm ngăn ngang của kệ sách.

2. ĐIỀU KIỆN ĐỂ HAI MẶT PHẲNG SONG SONG

Bài 1: Cho mặt phẳng (P) chứa hai đường thẳng...

Đáp án: 

a) Ta có: c,a,b ⊂ (P) 

Mà hai đường thẳng a,b cắt nhau nên c phải cắt ít nhất một trong hai đường thẳng a và b. Điều này trái với giả thiết a,b cùng song song với (Q).

b) Do (P) và (Q) không có điểm chung => (P)//(Q)

Bài 2: Cho tứ diện ABCD có E, F, H lần lượt...

Đáp án: 

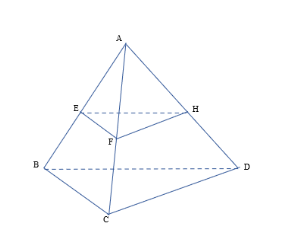
Ta có EF,FH lần lượt là đường trung bình của △ABC và △ACD

=> EF//BC,FH//CD. 

Mặt khác EF và FH cùng chứa trong (EFH),EF ∩ FH=F

=> (EFH)//(BCD).

3. TÍNH CHẤT CỦA HAI MẶT PHẲNG SONG SONG

Bài 1:

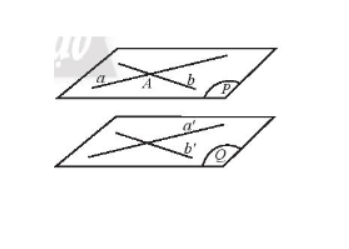
a) Cho điểm A ở ngoài mặt phẳng (Q)...

Đáp án: 

a) Vẽ a đi qua A và song song a' mà a' ⊂ (Q) nên thỏa mãn a // (Q).

Tương tự từ điểm A vẽ đường thẳng b song song với đường thẳng b’

b) Hai mặt phẳng này song song với nhau hay mp(a,b)//(Q).

Bài 2: Cho ba mặt phẳng...

Đáp án: 

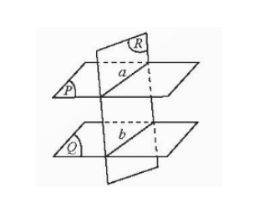
Ta có: (P) // (Q) và a ⊂ (P) nên a // (Q).

Mà (R) ∩ (Q) = b 

=> a//b.

Bài 3: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành...

Đáp án: 

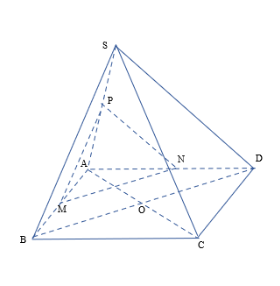
Gọi M, N, P lần lượt giao điểm của mặt phẳng ($\alpha$) với AB, AD và SA

Trong (ABCD) lần lượt cắt 2 mặt phẳng song song (α) và (SBD) tại MN và BD => MN//BD. Do đó $\frac{MN}{BD}=\frac{AM}{AB}=\frac{AN}{AD}$ (định lí Thales)

Trong (SAB) lần lượt cắt 2 mặt phẳng song song (α) và (SBD) tại MP và AB 

=> MP//AB. Do đó $\frac{MP}{SB}=\frac{AM}{AB}$ (định lí Thales)

Trong (SAD) lần lượt cắt 2 mặt phẳng song song (α) và (SBD) tại NP và AD 

=> NP//AD. Do đó $\frac{NP}{SD}=\frac{AN}{AB}$ (định lí Thales)

=> $\frac{MN}{BD}=\frac{MP}{SB}=\frac{NP}{SD}$

Mà △SBD đều nên SB = BD = SD

Vậy ta có: MN = MP = NP hay △MNP đều.

Bài 3: Khi dùng dao cắt các lớp bánh...

Đáp án: 

Mặt phẳng (P) cắt các mặt phẳng chứa các lớp bánh song song với nhau theo đó giao tuyến của (P) và các lớp bánh cũng song song với nhau.

4. ĐỊNH LÍ THASLES TRONG KHÔNG GIAN

Bài 1: Cho ba mặt phẳng song song (P), (Q), (R) lần lượt...

Đáp án: 

a) Trong △ACC', ta có BB₁ ∕∕CC' nên $\frac{AB}{BC}=\frac{AB₁}{B₁C'}$ (định lí Thales)

b) Trong △AA'C', ta có B'B₁ ∕∕AA' nên $\frac{AB1}{B1C'}=\frac{A'B'}{B'C'}$ (định lí Thales)

c) Ta có: $\frac{AB}{BC}=\frac{AB1}{B1C'}=\frac{A'B'}{B'C'}$ (cmt) 

=> $\frac{AB}{A'B'}=\frac{BC}{B'C'}=\frac{AC}{A'C'}$(tính chất dãy tỉ số bằng nhau)

Bài 2: Cho hình chóp S.ABC có...

Đáp án: 

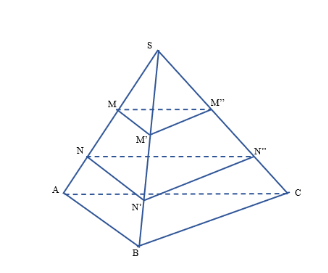
Trong △SAB có MM'//AB nên $\frac{SM}{SA}=\frac{SM'}{SB}$ => $SM'=\frac{SM.SB}{SA}=\frac{16}{3}$

Trong △SAB có NN'//AB nên$\frac{SN}{SA}=\frac{SN'}{SB}$ => $SN'=\frac{SN.SB}{SA}=\frac{28}{3}$

=> M'N'=SN'-SM'=4

Trong △SAC, có MM''//AC nên $\frac{SM}{SA}=\frac{SM''}{SC}$ => $SM''=\frac{SM.SC}{SA}=\frac{20}{3}$

Trong △SAC có NN''//AB nên $\frac{SN}{SA}=\frac{SN''}{SC}$ => $SN''=\frac{SM.SC}{SA}=\frac{35}{3}$

=> M''N''=SN''-SM''=5

=> $N''C=SC-SN''=\frac{10}{3}$. 

5. HÌNH LĂNG TRỤ VÀ HÌNH HỘP

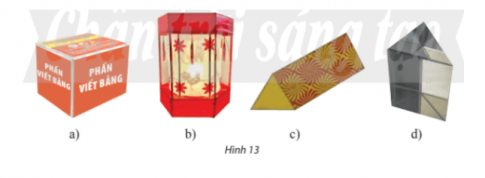
Bài 1: Hình dạng của các đồ vật như hộp phấn, lồng đèn, hộp quà, lăng kính có đặc điểm gì giống nhau?

Đáp án: 

+) Có hai đáy là hai mặt song song với nhau.

+) Các mặt bên là các hình chữ nhật.

+) Các cạnh bên có độ dài bằng nhau.

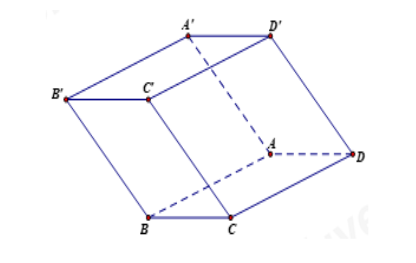
Bài 2: Cho hình lăng trụ…

Đáp án: 

Ta có: AB // CD, AD // BC (ABCD là hình bình hành)

a) (ABCD) // (A'B'C'D'), (ABB'A') cắt hai mặt phẳng đó lần lượt tại AB và A'B' nên AB // A'B'

Mà AA' // BB' nên ABB'A' là hình bình hành

Tương tự ta chứng minh được BCC'B', CDD'C', ADD'A' là hình bình hành

Ta có: 

• CD//C'D', A'B' // AB mà AB // CD => C'D' // A'B'
• B'C'//BC, A'D' // AD mà BC // AD => B'C' // A'D'

=> A'B'C'D' là hình bình hành

b) (ABCD) // (A'B'C'D'), (ACC'A') cắt hai mặt phẳng đó lần lượt tại AC và A'C' nên AC // A'C'

Mà AA'//CC' => ACC'A' là hình bình hành

Tương tự: BB'D'D là hình bình hành

c) ACC'A' là hình bình hành => AC', A'C là cắt nhau tại trung điểm mỗi đường 

BDD'B' là hình bình hành => BD', B'D là cắt nhau tại trung điểm mỗi đường 

Ta có (ABCD) // (A'B'C'D'), (ABC'D') cắt hai mặt phẳng đó lần lượt tại AB và C'D' => AB // C'D'

Mà ABCD là hình bình hành nên AB = DC; DCC'D' là hình bình hành nên DC = D'C'. Do dó AB = C'D'

Suy ra ABC'D' là hình bình hành. Nên AC' và BD' cắt nhau tại trung điểm mỗi đường 

=> A'C, AC', B'D, BD' có cùng trung điểm.

Bài 3: Cho hình hộp

Đáp án: 

Mặt phẳng ($\alpha$) cắt hai mặt phẳng song song (ABB'A') và (CDD'C') lần lượt tại NP và SR => NP // SR

Mặt phẳng ($\alpha$) cắt hai mặt phẳng song song (ADD'A') và (BDD'B') lần lượt tại MS và PQ => PQ // MS

Mặt phẳng ($\alpha$) cắt hai mặt phẳng song song (ABCD) và (A'B'C'D') lần lượt tại MN và QR => MN // QR

Bài 4: Tìm hình…

Đáp án: 

Hình hộp chữ nhật và hình lập phương

BÀI TẬP CUỐI SGK

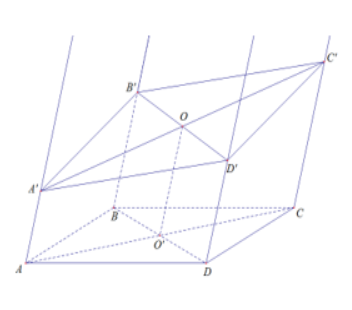
Bài 1: Trong mặt phẳng (P)…

Đáp án: 

Vì AB // CD => AB // (CDD'C'), AA' // DD' => DD' // (CDD'C')

Ta có (ABB'A') đi chứa 2 đường thẳng cắt nhau AB và AA' cùng song song với (CDD'C') nên (ABB'A') // (CDD'C')

AD // BC nên AD // (BCC'B'), AA' // BB' nên AA' // (BCC'B')

Ta có (ADD'A') đi chứa 2 đường thẳng cắt nhau AD và AA' cùng song song với (CBB'C') => (ADD'A')//(CBB'C')

Mặt phẳng (A'B'C'D') cắt hai mặt phẳng song song (ABB'A') và (CDD'C') lần lượt tại A'B' và CD' => AB' // CD' 

Mặt phẳng (A'B'C'D') cắt hai mặt phẳng song song (ADD'A') và (CBB'C') lần lượt tại A'D' và CB' nên AD' // CB' 

=> A'B'C'D' là hình bình hành, nên A'C' cắt B'D' tại trung điểm O

Gọi O' là giao của AC và BD

Mặt phẳng (AA'C'C) cắt hai mặt phẳng song song (ABB'A') và (CDD'C') lần lượt tại AA' và CC' nên AA'//CC' 

Trong hình thang ACC'A' có OO' là đường trung bình nên AA' + CC' = 2OO'

Mặt phẳng (BDD'B') cắt hai mặt phẳng song song (ABB'A') và (CDD'C') lần lượt tại BB' và DD' nên BB'//DD'

Trong hình thang BDD'B' có OO' là đường trung bình nên BB' + DD' = 2OO'

Vậy AA' + CC' = BB' + DD'

Bài 2: Cho hình chóp S.ABCD…

Đáp án: 

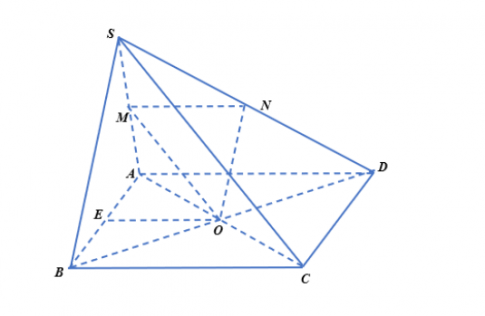
a) Trong △SBD có 

ON là đường trung bình => ON//SB 

=> MN//(SBC)

Trong △SAD có 

MN là đường trung bình => MN//AD. 

Mà AD//BC => MN//BC. => MN // (SBC)

 (OMN) chứa hai đường thẳng cắt nhau MN và ON cùng // (SBC)

=> (OMN) // (SBC)

b) Trong △ABC có OE là đường trung bình 

=> OE // BC => OE // (SBC)

Mà (OMN) // (SBC) nên E ∈ (OMN)

Ta có: (OMN) // (SBC); EF ⊂ (OMN) => EF // (SBC)

Bài 3: Cho hai hình vuông…

Đáp án: 

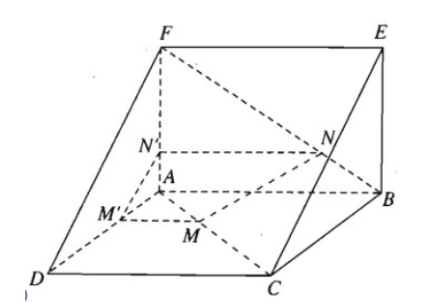
a) Ta có: 

AD//BC nên AD//(BEC)

AF//BE nên AF//(BEC)

 (ADF) đi qua hai đường thẳng cắt nhau AD và AF cùng // (CBE) 

=> (ADF) // (CBE)

b) Vì ABCD và ABEF là hình vuông có cạnh bằng nhau => AC = BF

Trong △ADC có MM'//CD => $\frac{AM'}{AD}=\frac{AM}{AC}$ 

Trong △ABF có NN'//AB => $\frac{AN'}{AF}=\frac{BN}{BF}$ 

Mà AM = BN nên $\frac{AN'}{AF}=\frac{AM'}{AD}$ . 

=> M'N'//DF => M'N' // (DEF)

Ta có MM'//AB//EF nên MM'//(DEF)

 (MNN'M') chứa hai đường thẳng cắt nhau MM' và M'N' cùng // với (DEF) 

Do đó, (MNN'M') // (DEF)

Bài 4: Cho hình hộp…

Đáp án: 

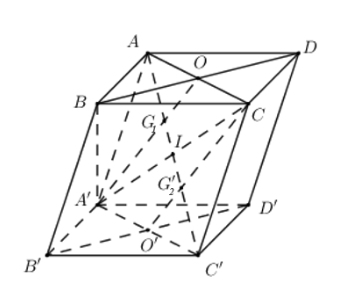
Gọi O là giao điểm của AC và BD, O' là giao điểm của A'C' và B'D', I là giao điểm của AC' và A'C

Do ACCA' là hình bình hành nên I là trung điểm của A'C

G1 là trọng tâm △BDA' nên $\frac{A'G'_{1}}{AO}=\frac{2}{3}$

△AA'C có A'O là trung tuyến, $\frac{A'G'_{1}}{AO}=\frac{2}{3}$  nên G₁ là trọng tâm của △AA'C.

Mà I là trung điểm A'C nên G₁ ∈ AI và $AG_{1} = \frac{2}{3}AI$

Mà $AI = \frac{1}{2}AC′$ nên $AG_{1} = \frac{2}{3}AC'$

Tương tự ta có $C'G_{2} = \frac{1}{3}AC$

=> G₁, G₂ chia AC' thành 3 đoạn thẳng bằng nhau

Bài 5: Để làm một khung…

Đáp án: 

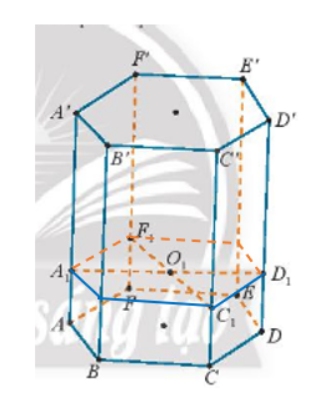
a) Do (A₁C₁D₁F₁) chứa  A₁D₁ và C₁F₁ cắt nhau và cùng // (ABCDEF)

Nên (A1C1D1F1)  // (ABCDEF)

Gọi B₁,E₁ lần lượt là giao của (A1C1D1F1) với BB' và EE'

Ta có giao tuyến của (A1C1D1F1) với các mặt bên của lăng trụ là A₁B₁, B₁C₁, C₁D₁, D₁E₁, E₁F₁, F₁A₁

b) Ta có: A′A₁ = 6AA₁; AA′ = 70 nên AA₁ = 10

Do (ACC'A') cắt (A1C1D1F1) // (ABCDEF) lần lượt tại A₁C₁ và AC nên A1C1 // AC

Mà AA₁ // CC₁ => AA₁C₁C là hình bình hành. 

=> CC₁ = AA₁ = 10

Mà CC' = AA' = 70

Nên C₁C′ = 70 – 10 = 60

Bài 6: Chỉ ra các mặt phẳng song song…

Đáp án: 

Hình a: các mặt tấm pin song song với nhau

Hình b: Các mặt của toà nhà song song với nhau

Một số ví dụ khác về mặt phẳng song song: mặt của các bậc cầu thang, mặt phẳng của các bức tường đối diện nhau