1. GÓC LƯỢNG GIÁC

Bài 1: Một chiếc bánh lái tàu có thể quay theo cả hai chiều. Trong Hình 1 và Hình 2, lúc đầu thanh OM ở vị trí OA….

Đáp án:

a) 

b) 

Bài 2: Cho...

Đáp án:

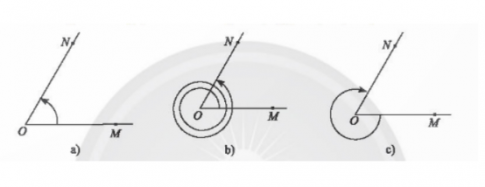
a) Góc lượng giác (OM,ON) = 60$^{\circ}$;
b) Góc lượng giác (OM,ON) = 60$^{\circ}$+2⋅360$^{\circ}$=780$^{\circ}$;
c) Góc lượng giác (OM,ON) = -300$^{\circ}$.

Bài 3: Trong các khoảng thời gian từ 0 giờ đến 2 giờ 15 phút, kim phút quét một góc lượng giác là bao nhiêu độ?

Đáp án:

Đổi 2 giờ 15 phút = $2\frac{1}{4}$ giờ

Kim phút quay $2\frac{1}{4}$ vòng theo chiều âm nên kim phút đã quét được góc lượng giác là: $\alpha $=-$2\frac{1}{4}$.360$^{\circ}$=-810$^{\circ}$.

Bài 4: Cho Hình 7….

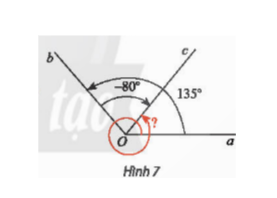
Đáp án:

a) Số đo góc lượng giác (Oa,Ob) = 135$^{\circ}$.

Số đo góc lượng giác (Ob,Oc) = -80$^{\circ}$.

aOc=135$^{\circ}$-80$^{\circ}$=55$^{\circ}$. Mà góc lượng giác (Oa,Oc) tương ứng với chuyển động quay theo chiều dương từ Oa đến Oc, sau đó quay thêm 1 vòng. 

=> Số đo góc lượng giác (Oa,Oc) = 55$^{\circ}$+360$^{\circ}$=415$^{\circ}$.

b) Như vậy đối với ba góc trong hình, ta có tổng số đo góc lượng giác (Oa,Ob) và (Ob,Oc) chênh lệch với số đo góc lượng giác (Oa,Oc) là một số nguyên lần 360$^{\circ}$.

Bài 5: Trong Hình 8, chiếc quạt có 3 cánh được phân bố đều nhau. Viết công thức tổng quát số đo của góc lượng giác (Ox, ON) và (Ox, OP).

Đáp án:

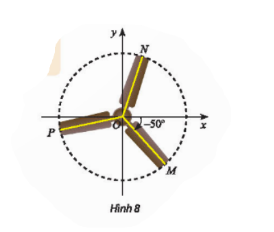
$\widehat{MON}=\widehat{MON}$=$\frac{1}{3}$.360$^{\circ}$=120$^{\circ}$.  

Số đo các góc lượng giác (OM,ON) và (OM,OP) lần lượt là 120$^{\circ}$ và -120$^{\circ}$.

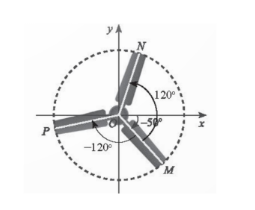
(Ox,ON)  =(Ox,OM)+(OM,ON)+k360$^{\circ}$($k\in Z$)   =-50$^{\circ}$+120$^{\circ}$+k360$^{\circ}$($k\in Z$)   =70$^{\circ}$+k360$^{\circ}$($k\in Z$).

(Ox,OP)  =(Ox,OM)+(OM,OP)+k360$^{\circ}$($k\in Z$)   =-50$^{\circ}$-120$^{\circ}$+k360$^{\circ}$($k\in Z$)   =-170$^{\circ}$+k360$^{\circ}$($k\in Z$).

2. ĐƠN VỊ RADIAN

Bài 1: Vẽ đường tròn tâm O bán kính R bất kì. Dùng một đoạn dây mềm đo bán kính và đánh dấu được…

Đáp án:

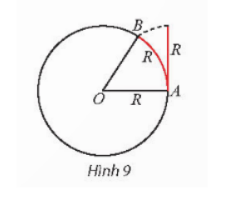
$\widehat{AOB}$ bằng khoảng 57$^{\circ}$.

Bài 2: Hoàn thành bảng chuyển đổi đơn vị đo của các góc sau đây:…

Đáp án:

3. ĐƯỜNG TRÒN LƯỢNG GIÁC

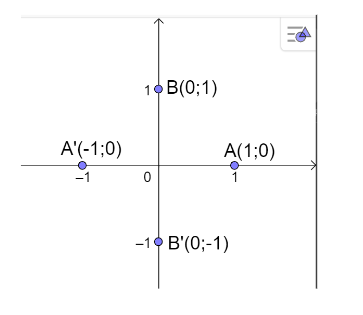
Bài 1: Trong mặt phẳng toạ độ Oxy, vẽ đường tròn tâm O bán kính bằng 1 và...

Đáp án:

a) (OA,OB)=90$^{\circ}$=$\frac{\pi}{2}$+$k2\pi$ rad,$k\in Z$

b) A'(-1;0) và B'(0;-1).

Bài 2: Biểu diễn trên đường tròn lượng giác các góc lượng giác có số đo...

Đáp án:

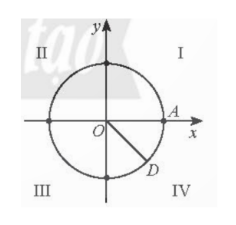
a) -1485$^{\circ}$=-45$^{\circ}$-4.360$^{\circ}$.

Vậy điểm biễu diễn góc lượng giác có số đo -148$^{\circ}$5 là điểm D trên đường tròn lượng giác thuộc góc phần tư thứ IV khi $\widehat{AOD}$=45$^{\circ}$. 

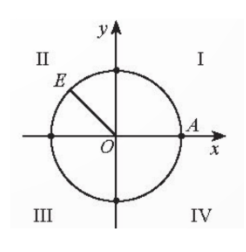
b) $\frac{19\pi}{4}$=$\frac{3\pi}{4}$+$4\pi$

Vậy điểm biểu diễn góc lượng giác có số đo  $\frac{19\pi}{4}$ là điểm E trên đường tròn lượng giác thuộc góc phần tư thứ II khi $\widehat{AOE}$=$\frac{3\pi}{4}$.

4. GIẢI BÀI TẬP CUỐI SGK

Bài 1: Đổi số đo của các góc sau đây sang radian:

Đáp án:

Bài 2: Đổi số đo của các góc sau đây sang...

Đáp án:

Bài 3: Biểu diễn các góc lượng giác sau trên đường tròn...

Đáp án:

a) $\frac{-17\pi}{3}$=$\frac{\pi}{3}$-$3.2\pi$

Vậy điểm biểu diễn góc lượng giác có số đo $\frac{-17\pi}{3}$ là điểm M trên đường tròn lượng giác thuộc góc phần tư thứ I khi $\widehat{AOM}$=$\frac{\pi}{3}$.

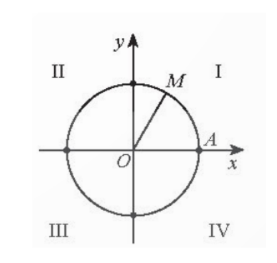
b)  $\frac{13\pi}{4}$=$\frac{-3\pi}{4}$-$2.2\pi$

Vậy điễm biểu diễn góc lượng giác có số đo $\frac{13\pi}{4}$ là điểm N trên đường tròn lượng giác thuộc góc phần tư thứ III khi $\widehat{AON}$=$\frac{-3\pi}{4}$.

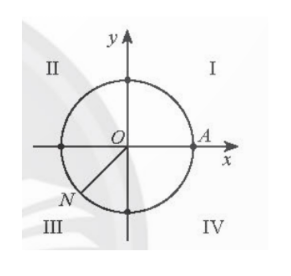
c) -765$^{\circ}$=-45$^{\circ}$-2⋅360$^{\circ}$.

Vậy điểm biểu diễn góc lượng giác có số đo -765$^{\circ}$ là điểm P trên đường tròn lượng giác thuộc góc phần tư thứ IV khi $\widehat{AOP}$=45$^{\circ}$.

Bài 4: Góc lượng...

Đáp án:

$\frac{31\pi}{7}$=$\frac{3\pi}{7}$+$4\pi$; 

$\frac{31\pi}{7}$=$\frac{10\pi}{7}$+$3\pi$; 

$\frac{31\pi}{7}$=$\frac{-25\pi}{7}$+$8\pi$.

=> $\frac{31\pi}{7}$ có cùng điểm biểu diễn với góc lượng giác $\frac{3\pi}{7}$ và $\frac{-25\pi}{7}$.

Bài 5: Viết công thức số đo tổng quát của các...

Đáp án:

(OA,OM)=120$^{\circ}$+k360$^{\circ}$ ($k\in Z$)

(OA,ON)=-75$^{\circ}$+k360$^{\circ}$ ($k\in Z$)

Bài 6: Viết công thức số đo tổng quát của...

Đáp án:

(OM,ON)=(Ox,OM)+(Ox,ON)+k360$^{\circ}$($k\in Z$) 

2.72$^{\circ}$=45$^{\circ}$ +(Ox,ON)+k360$^{\circ}$($k\in Z$)    

=> (Ox,ON) = =99$^{\circ}$+k360$^{\circ}$($k\in Z$).

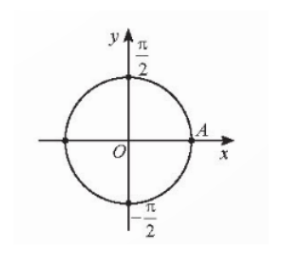
Bài 7: Trên đường tròn lượng giác, hãy biểu diễn các góc lượng giác có số...

Đáp án:

a)

b) 

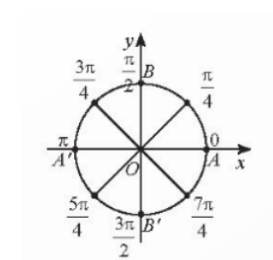
Bài 8: Vị trí các điểm B, C, D trên cánh quạt động cơ...

Đáp án:

$\frac{\pi}{2}$+k$\frac{2\pi}{3}$($k\in Z$) và $-\frac{\pi}{6}$+k$\frac{2\pi}{3}$($k\in Z$).

Bài 9: Hải li là một đơn vị chiều dài hàng hải, được tính bằng...

Đáp án:

Ta có $\alpha$=$\frac{1}{60}$.$\frac{\pi}{180}$=$\frac{\pi}{10800}$(rad).

Một hài lí có độ dài là: $\frac{\pi}{10800}$⋅6371≈1,85( km).