Bài 63 trang 31 SBT Toán 11 Tập 1: Cho lục giác đều ABCDEF nội tiếp trong đường tròn lượng giác (thứ tự đi từ A đến các đỉnh theo chiều dương). Khi đó, số đo của góc lượng giác (OA, OC) bằng:

A. $\frac{2\pi }{3}$+k2π.

B. −$\frac{2\pi }{3}$+k2π

C. $\frac{\pi }{3}$+k2π

D. −$\frac{\pi }{3}$+k2π

Lời giải:

Đáp án đúng là: A

Vì ABCDEF là lục giác đều nên

ˆAOB=ˆBOC=ˆCOD=ˆDOE=ˆEOF=ˆFOA=60°=$\frac{\pi }{3}$

Khi đó, ta có: (OA,OC)=$ \frac{\pi }{3}+\frac{\pi }{3}+k2π=\frac{2\pi }{3}$ +   k2π

Bài 64 trang 31 SBT Toán 11 Tập 1: Cho tan α = 2. Giá trị của biểu thức A= $\frac{3sin\alpha +cos\alpha }{sin\alpha -cos\alpha }$ bằng:

Lời giải:

Vì tan α = 2 xác định nên cos α ≠ 0. Chia cả tử và mẫu của A cho cos α ta được:

A= $\frac{3sin\alpha +cos\alpha }{sin\alpha -cos\alpha }=\frac{3tan\alpha+1}{tan\alpha -1}=\frac{3.2+1}{2-1}=7$
Bài 65 trang 32 SBT Toán 11 Tập 1: Giá trị của biểu thức A = (2sin x – cos x)² + (2cos x + sin x)² bằng:

A. 5.

B. 3.

C. 4.

D. 2.  

Lời giải:

Đáp án đúng là: A

Ta có A = (2sin x – cos x)² + (2cos x + sin x)²

= 4sin² x – 4sin x cos x + cos² x + 4cos² x + 4cos x sin x + sin² x

= 5sin² x + 5cos² x

= 5(sin² x + cos² x)

= 5 . 1 = 5.

Bài 66 trang 32 SBT Toán 11 Tập 1: Nếu hai góc a và b có tan a = $\frac{1}{3}$  và tan b = $\frac{1}{2}$  thì giá trị của tan(a – b) bằng:

A. $\frac{1}{7}$

B. -$\frac{1}{5}$

C. -$\frac{1}{7}$

D. 1.

Lời giải:

Đáp án đúng là: C

Ta có tan(a−b)=$ \frac{tana-tanb}{1+tanatanb}=\frac{\frac{1}{3}-\frac{1}{2}}{1+\frac{1}{3}.\frac{1}{2}}=-\frac{1}{7}$
Bài 67 trang 32 SBT Toán 11 Tập 1: Nếu cos2α =$\frac{\sqrt{3}}{6}$ thì giá trị của biểu thức cos(α+$\frac{\pi }{3}$)cos(α−$\frac{\pi }{3}$) bằng:

A. $\frac{\sqrt{3}}{3}$

B. $\frac{-3+\sqrt{3}}{12}$

C. -$\frac{\sqrt{3}}{3}$

D. $\frac{3+\sqrt{3}}{12}$

Lời giải:

Đáp án đúng là: B

Ta có: cos(α+$\frac{\pi }{3}$)cos(α−$\frac{\pi }{3}$)

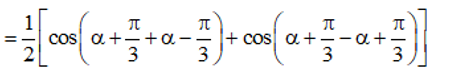
=12(cos2α+cos$ \frac{2\pi }{3}$)

=$ \frac{1}{2}(\frac{\sqrt{3}}{6}-\frac{1}{2})=\frac{-3+\sqrt{3}}{12}$

Bài 68 trang 32 SBT Toán 11 Tập 1: Phương trình cos 2x = 0 có các nghiệm là:

A. x=$ \frac{\pi }{2}$+kπ(k∈Z)

B. x=$ \frac{\pi }{4}$+kπ(k∈Z)

C. x=$ \frac{\pi }{4}$+kπ2(k∈Z)

D. x=kπ(k∈Z)

Lời giải:

Đáp án đúng là: C

Ta có cos 2x = 0 ⇔2x=$ \frac{\pi }{2}$+kπ(k∈Z) ⇔x=$ \frac{\pi }{4}+k \frac{\pi }{2}$(k∈Z)

Bài 69 trang 32 SBT Toán 11 Tập 1: Phương trình tan x = có các nghiệm là: 

A. x=$ \frac{\pi }{6}$+kπ(k∈Z)

B. x=−$ \frac{\pi }{6}$+kπ(k∈Z).

C. x=$ \frac{\pi }{3}$+kπ(k∈Z)

D. x=−$ \frac{\pi }{3}$+kπ(k∈Z)

Lời giải:

Đáp án đúng là: B

Do tan(−$\frac{\pi }{6}$) nên tan x = −$ \frac{1}{\sqrt{3}}$⇔tanx=tan(−$\frac{\pi }{6}$)

⇔x=−$ \frac{\pi }{6}$+kπ(k∈Z).

Bài 70 trang 32 SBT Toán 11 Tập 1: Chứng minh mỗi đẳng thức sau là đúng:

a) sin 45° . cos 30° + cos(– 45°) . sin(– 30°) = sin 15°;

b) tan$ \frac{9\pi }{20}$ =$ \frac{1+tan\frac{\pi }{5}}{1-tan\frac{\pi }{5}}$

Lời giải:

a) Ta có VT = sin 45° . cos 30° + cos(– 45°) . sin(– 30°)

                   = sin 45° . cos 30° + cos 45° . (– sin 30°)

= sin 45° . cos 30° – cos 45° . sin 30°

= sin(45° – 30°)

= sin 15° = VP  (đpcm).

b) Ta có tan$ \frac{9\pi }{20}$  =$ tan(\frac{\pi }{4}+\frac{\pi }{5})$ =$ \frac{tan\frac{\pi }{4}+tan\frac{\pi }{5}}{1-tan\frac{\pi }{4}.tan\frac{\pi }{5}}=\frac{1+tan\frac{\pi }{5}}{1-tan\frac{\pi }{5}}$

Vậy tan$ \frac{9\pi }{20}$=$\frac{1+tan\frac{\pi }{5}}{1-tan\frac{\pi }{5}}$ (đpcm).

Bài 71 trang 32 SBT Toán 11 Tập 1: Cho sin(45°– α) = $\frac{1}{2\sqrt{2}}$

a) Chứng minh rằng sin²(45°−α)=$ \frac{1-sin2\alpha }{2}$

b) Tính sin 2α.

Lời giải:

a) Sử dụng công thức hạ bậc và quan hệ lượng giác của hai góc phụ nhau, ta có:

sin²(45°−α)=$\frac{1-cos(90^{\circ}-2\alpha )}{2}=\frac{1-sin2\alpha }{2}$

Vậy sin²(45°−α)= $ \frac{1-sin2\alpha }{2}$ (đpcm).

b) Vì sin(45°– α) = $\frac{1}{2\sqrt{2}}$ nên sin²(45°– α) = $(\frac{1}{2\sqrt{2}})^{2}$=$\frac{1}{8}$

Theo câu a) ta có sin²(45°−α)= $ \frac{1-sin2\alpha }{2}$ , do đó $ \frac{1-sin2\alpha }{2}$ = $\frac{1}{8}$

Từ đó suy ra sin2α=$\frac{3}{4}$

Bài 72 trang 32 SBT Toán 11 Tập 1: Giải phương trình:

a) sin(2x−$\frac{\pi }{6}$)=$-\frac{1}{2}$

b) sin(x3+$\frac{\pi }{2}$)=$\frac{\sqrt{3}}{2}$

c) cos(2x+$\frac{\pi }{5}$)=$\frac{\sqrt{2}}{2}$

d) 2cos$\frac{x}{2}$+$\sqrt{3}$=0

e)  tan(2x+$\frac{\pi }{3}$)−1=0

g) cot(3x + π) = – 1.

Lời giải:

a) Do sin($-\frac{\pi }{6}$)=−$\frac{1}{2}$ nên sin(2x−$\frac{\pi }{6}$)=−$\frac{1}{2}$ ⇔sin(2x−$\frac{\pi }{6}$)=sin(−$\frac{\pi }{6}$)

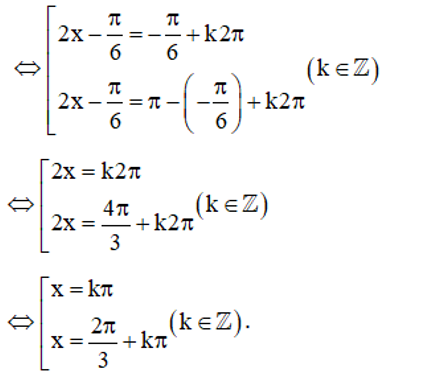
b) Do sin$\frac{\pi }{3}$=$\frac{\sqrt{3}}{2}$ nên sin(x3+\frac{\pi }{2})=$\frac{\sqrt{3}}{2}$ ⇔$ sin(x3+\frac{\pi }{2})=sin \frac{\pi }{2}$

c) Do cos$ \frac{\pi }{4}$=$ \frac{\sqrt{2}}{2}$ nên  cos(2x+$ \frac{\pi }{5})$⇔ cos(2x+$ \frac{\pi }{5})$=$cos \frac{\pi }{4}$

d) 2cos$ \frac{x}{2}$+$ \sqrt{3}$=0

⇔cos$ \frac{x}{2}$=$ -\frac{\sqrt{3}}{2}$

⇔ cos$ \frac{x}{2}$=cos$ \frac{5\pi }{6}$ (do cos$ \frac{5\pi }{6}$ = $-\frac{\sqrt{3}}{2}$)

e) $\sqrt{3}$tan(2x+$\frac{\pi }{3}$)−1=0

⇔tan(2x+$\frac{\pi }{3}$)=$\frac{1}{\sqrt{3}}$

⇔tan(2x+$\frac{\pi }{3}$)=tan$\frac{\pi }{6}$ (do tan$\frac{\pi }{6}$=$\frac{1}{\sqrt{3}}$)

⇔2x+$\frac{\pi }{3}$=$\frac{\pi }{6}$+kπ(k∈Z)

⇔2x=−$\frac{\pi }{6}$+kπ(k∈Z)

⇔x=−$\frac{\pi }{12}$+k$\frac{\pi }{2}$(k∈Z).

g) Do cot($-\frac{\pi }{4}$)=−1 nên cot(3x + π) = – 1 ⇔cot(3x+π)=cot($-\frac{\pi }{4}$)

⇔3x+π=$-\frac{\pi }{4}$+kπ(k∈Z)

⇔3x=$-\frac{5\pi }{4}$+kπ(k∈Z)

⇔x=$-\frac{5\pi }{12}$+k$\frac{\pi }{3} $(k∈Z).

Bài 73 trang 33 SBT Toán 11 Tập 1: Giải phương trình:

a) sin(2x+$\frac{\pi }{3}$)=sin(3x−$\frac{\pi }{6}$)

b) cos(x+$\frac{\pi }{4}$)=cos($\frac{\pi }{4}$−2x)

c) cos²($\frac{x}{2}$+$\frac{\pi }{6}$)=cos²($\frac{3x}{2}$+$\frac{\pi }{4}$)

d) cot3x=tan$\frac{2\pi }{7}$

Lời giải:

a) sin(2x+$\frac{\pi }{3}$)=sin(3x−$\frac{\pi }{6}$)

b) cos(x+$\frac{\pi }{4}$)=cos($\frac{\pi }{4}$−2x)

c) Sử dụng công thức hạ bậc ta có:

cos²($\frac{x}{2}$+$\frac{\pi }{6}$)=cos²($\frac{3x}{2}$+$\frac{\pi }{4}$)

⇔ $\frac{1+cos(x+\frac{\pi }{3})}{2}=\frac{1+cos(3x+\frac{\pi }{2})}{2}$

⇔cos(x+$ \frac{\pi }{3}$)=cos(3x+$ \frac{\pi }{2}$)

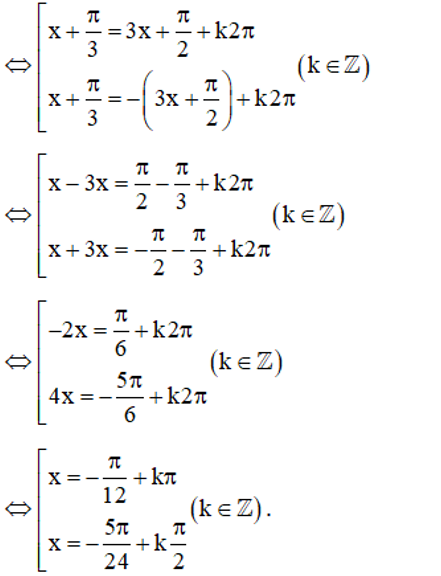
d) Sử dụng quan hệ phụ nhau của hai góc lượng giác, ta có:

cot3x=tan$\frac{2\pi }{7}$

⇔cot3x=cot($\frac{\pi }{2}− \frac{2\pi }{7}$)

⇔cot3x=cot$ \frac{3\pi }{14}$

⇔3x=$ \frac{3\pi }{14}$+kπ(k∈Z)

⇔x=$ \frac{\pi }{14}$+k$ \frac{\pi }{3}$(k∈Z)

Bài 74 trang 33 SBT Toán 11 Tập 1: Một chất điểm chuyển động đều theo chiều ngược chiều kim đồng hồ trên đường tròn bán kính 5 cm. Khoảng cách h (cm) từ chất điểm đến trục hoành được tính theo công thức h = |y|, trong đó y=asin($\frac{\pi }{5}t$)  với t là thời gian chuyển động của chất điểm tính bằng giây (t ≥ 0) và chất điểm bắt đầu chuyển động từ vị trí A (Hình 16).

a) Chất điểm chuyển động một vòng hết bao nhiêu giây?

b) Tìm giá trị của a.

c) Tìm thời điểm sao cho chất điểm ở vị trí có h = 2,5 cm và nằm phía dưới trục hoành trong một vòng quay đầu tiên.

Lời giải:

a) Xét h = 0 hay |y| = 0, suy ra y = 0, tức là asin($\frac{\pi }{5}t$)=0⇔sin($\frac{\pi }{5}t$)=0

⇔$ \frac{\pi }{5}t$=kπ(k∈Z) ⇔t=5k(k∈Z,k≥0 (do t ≥ 0).

Ta nhận thấy, từ thời điểm ban đầu, cứ sau 5 giây, khoảng cách từ chất điểm đến trục hoành lại bằng 0. Suy ra sau mỗi 5 giây, chất điểm chuyển động được nửa vòng. Vậy chất điểm chuyển động một vòng hết 10 giây.

b) Do chất điểm chuyển động một vòng hết 10 giây nên khi t = 2,5 giây thì chất điểm chuyển động được một phần tư vòng theo chiều dương, suy ra tại t = 2,5 ta có y = |y| = h = 5 (do bằng bán kính). Khi đó, asin($\frac{\pi }{5}$.2,5)=5.

Vậy a = 5.

c) Từ kết quả câu b, ta có: y=5sin($\frac{\pi }{5}t$).

Do h = 2,5 cm và chất điểm nằm ở dưới trục hoành nên y = – 2,5.

Với y = – 2,5, ta có: 5sin($\frac{\pi }{5}t$)=−2,5

⇔sin($\frac{\pi }{5}t$)=$ -\frac{1}{2}$

⇔sin($\frac{\pi }{5}t$)=sin(−$\frac{\pi }{6}$)

Với vòng quay đầu tiên thì 0 ≤ t ≤ 10, do đó t=$ \frac{35}{6}$, t=.$ \frac{55}{6}$

Vậy tại thời điểm t=$ \frac{35}{6}$giây, t=$ \frac{55}{6}$giây thì chất điểm ở vị trí có h = 2,5 cm và nằm ở dưới trục hoành trong một vòng quay đầu tiên.