Bài 15 trang 50 SBT Toán 11 Tập 1: Trong các dãy số (u_n) với số hạng tổng quát sau, dãy số nào là cấp số cộng?

A. u_n = 3ⁿ.

B. u_n = 1 – 3n.

C. u_n = 3ⁿ + 1.

D. u_n = 3 + n².  

Lời giải:

Đáp án đúng là: B

Xét từng đáp án, ta thấy dãy số ở đáp án B là cấp số cộng.

Thật vậy, ta có u_n – u_{n – 1} = (1 – 3n) – [1 – 3(n – 1)] = 1 – 3n – 1 + 3n – 3 = – 3 luôn không đổi với mọi n ∈ ℕ* và u₁ = 1 – 3 . 1 = – 2.

Vậy (un) với u_n = 1 – 3n là một cấp số cộng với số hạng đầu u₁ = – 2 và công sai d = – 3. 

Bài 16 trang 50 SBT Toán 11 Tập 1: Cho cấp số cộng (u_n) biết u₁=$ \frac{1}{3}$; u₈ = 26. Công sai d của cấp số cộng đó là:

A. $ \frac{11}{3}$

B. $ \frac{10}{3}$

C. $ \frac{3}{13}$

D. $ \frac{3}{11}$

Lời giải:

Đáp án đúng là: A

Gọi d là công sai của cấp số cộng.

Ta có u₈ = u₁ + (8 – 1)d = u₁ + 7d.

Mà u₁=$ \frac{1}{3}$; u₈ = 26 nên ta có 26 = $ \frac{1}{3}$ + 7d, từ đó suy ra d =  $ \frac{11}{3}$

Bài 17 trang 50 SBT Toán 11 Tập 1: Viết ba số hạng xen giữa các số 2 và 22 để được một cấp số cộng có năm số hạng. Ba số hạng đó lần lượt là:

A. 7; 12; 17.

B. 6; 10; 14.

C. 8; 13; 18.

D. 6; 12; 18.

Lời giải:

Đáp án đúng là: A

Giả sử cấp số cộng có số hạng đầu u₁ = 2, công sai d, ba số hạng xen giữa 2 và 22 lần lượt là u₂, u₃, u₄ và số hạng thứ năm là u₅ = 22.

Khi đó ta có u₅ = u₁ + (5 – 1)d = 2 + 4d = 22, suy ra d = 5.

Do đó, u₂ = u₁ + d = 2 + 5 = 7; u₃ = u₂ + d = 7 + 5 = 12 và u₄ = u₃ + d = 12 + 5 = 17.

Vậy ba số hạng cần tìm là 7; 12; 17.

Bài 18 trang 50 SBT Toán 11 Tập 1: Cho cấp số cộng (u­_n) biết u₅ + u₇ = 19. Giá trị của u₂ + u₁₀ là:

A. 38.

B. 29.

C. 12.

D. 19.

Lời giải:

Đáp án đúng là: D

Giả sử d là công sai của cấp số cộng (u_n).

Ta có u₅ + u₇ = [u₁ + (5 – 1)d] + [u₁ + (7 – 1)d] = 2u₁ + 10d.

Và u₂ + u₁₀ = (u₁ + d) + [u₁ + (10 – 1)d] = 2u₁ + 10d.

Do đó, u₂ + u₁₀ = u₅ + u₇ = 19.

Bài 19 trang 50 SBT Toán 11 Tập 1: Cho (u_n) là cấp số cộng có số hạng đầu u₁ = 2, công sai d = − 5. Tổng 10 số hạng đầu của cấp số cộng đó là:

A. – 410.

B. – 205.

C. 245.

D. – 230.

Lời giải:

Đáp án đúng là: B

Tổng 10 số hạng đầu của cấp số cộng đó là:

S₁₀=$ \frac{(2u_{1}+(10-1)d).10}{2}=\frac{(2.2+9.(-5)).10}{2}=-205$

Bài 20 trang 50 SBT Toán 11 Tập 1: Cho (u_n) là cấp số cộng có S_n = n² + 4n với n ∈ ℕ*. Số hạng đầu u₁ và công sai d của cấp số cộng đó là:

A. u₁ = 3, d = 2.

B. u₁ = 5, d = 2.

C. u₁ = 8, d = – 2.

D. u₁ = – 5, d = 2.

Lời giải:

Đáp án đúng là: B

Ta có S₁ = 1² + 4 . 1 = 5 = u₁;

S₂ = 2² + 4 . 2 = 12, mà S₂ = u₁ + u₂ = 5 + u₂, từ đó suy ra u₂ = 12 – 5 = 7.

Do đó, công sai d của cấp số cộng là d = u₂ – u₁ = 7 – 5 = 2.

Vậy u₁ = 5, d = 2.

Bài 21 trang 50 SBT Toán 11 Tập 1: Cho ba số  $ \frac{1}{b+c},\frac{1}{c+a},\frac{1}{a+b}$ theo thứ tự lập thành cấp số cộng. Chứng minh rằng ba số a², b², c² theo thứ tự cũng lập thành một cấp số cộng.

Lời giải:

Do ba số  $ \frac{1}{b+c},\frac{1}{c+a},\frac{1}{a+b}$ theo thứ tự lập thành một cấp số cộng nên

⇔$ \frac{1}{c+a}-\frac{1}{b+c}=\frac{1}{a+b}-\frac{1}{c+a}$

⇔$ \frac{2}{c+a}=\frac{1}{a+b}+\frac{1}{b+c}$

⇔$ \frac{2}{c+a}=\frac{b+c+a+b}{(a+b)(b+c)}$

⇔$\frac{2}{c+a}=\frac{2b+c+a}{(a+b)(b+c)}$

⇒ 2(a + b)(b + c) = (c + a)(2b + c + a)

⇔ 2ab + 2ac + 2b² + 2bc = 2bc + c² + ca + 2ab + ac + a²

⇔ 2b² = a² + c²

⇔ b² – a² = c² – b².

Suy ra ba số a², b², c² theo thứ tự cũng lập thành một cấp số cộng.

Bài 22 trang 50 SBT Toán 11 Tập 1: Tìm x để ba số 10 – 3x, 2x² + 3, 7 – 4x theo thứ tự lập thành một cấp số cộng.

Lời giải:

Ba số 10 – 3x, 2x² + 3, 7 – 4x theo thứ tự lập thành một cấp số cộng khi

(2x² + 3) – (10 – 3x) = (7 – 4x) – (2x² + 3)

⇔ 2x² + 3 – 10 + 3x = 7 – 4x – 2x² – 3

⇔ 4x² + 7x – 11 = 0

Vậy thì thỏa mãn yêu cầu bài toán.

Bài 23 trang 50 SBT Toán 11 Tập 1: Tìm số hạng đầu và công sai của cấp số cộng (u_n), biết:

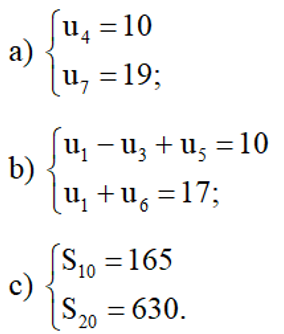
Lời giải:

a)    Ta có:

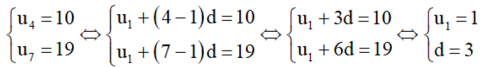
Vậy cấp số cộng đã cho có số hạng đầu u₁ = 1 và công sai d = 3.

b)    Ta có

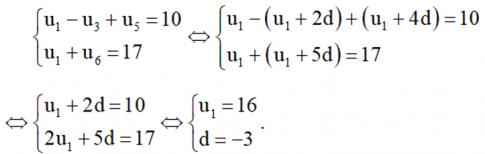
Vậy cấp số cộng đã cho có số hạng đầu u₁ = 16 và công sai d = – 3.

c)    Ta có

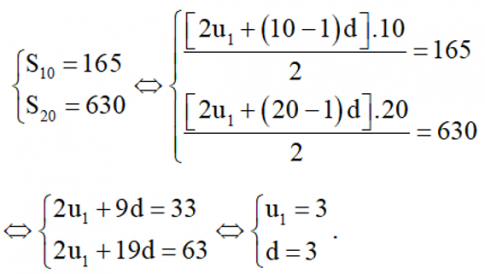
Vậy cấp số cộng đã cho có số hạng đầu u₁ = 3 và công sai d = 3.

Bài 24 trang 50 SBT Toán 11 Tập 1: Cho (u_n) là cấp số cộng có u₂ + u₄ = 22, u1 . u₅ = 21 và công sai d dương.

a) Tính u₁₀₀, S₁₀₀.

b) Tính tổng: u₁ + u₅ + u₉ + ... + u₁₀₁.  

Lời giải:

Ta có u₂ + u₄ = (u₁ + d) + (u₁ + 3d) = 2u₁ + 4d = 22, suy ra 4d = 22 – 2u₁.

Lại có u₁ . u₅ = u₁ . (u₁ + 4d) = u₁ . (u₁ + 22 – 2u₁) = u₁ . (22 – u₁).

Mà u₁ . u₅ = 21, do đó u₁ . (22 – u₁) = 21 ⇔ 22u₁ – u₁² – 21 = 0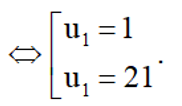 

Với u₁ = 1, suy ra d=$ \frac{22-2u_{1}}{4}=\frac{22-2.1}{4}=5>0$ (thỏa mãn).

Với u₁ = 21, suy ra d=$ \frac{22-2u_{1}}{4}=\frac{22-2.21}{4}=-5<0$ (không thỏa mãn).

Vậy cấp số cộng (u_n) có số hạng đầu u₁ = 1 và công sai d = 5.

a) Ta có: u₁₀₀ = u₁ + (100 – 1)d = 1 + 99 . 5 = 496.

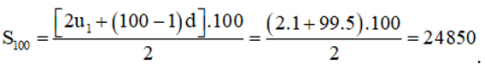
b) Ta có u₅ – u₁ = (u₁ + 4d) – u₁ = 4d, tương tự u₉ – u₅ = 4d, ...

Do đó các số u₁, u₅, u₉, ..., u₁₀₀ lập thành một cấp số cộng có số hạng đầu u₁ = 1 và công sai d' = 4d = 4 . 5 = 20.

Lại có (101 – 1) : 4 + 1 = 26 nên tổng u₁ + u₅ + u₉ + ... + u₁₀₁ gồm 26 số hạng.

Do vậy, u₁ + u₅ + u₉ + ... + u₁₀₁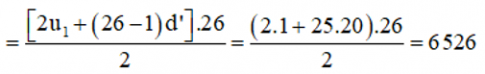 

Bài 25 trang 50 SBT Toán 11 Tập 1: Tìm năm số hạng liên tiếp của một cấp số cộng, biết tổng của chúng bằng 40 và tổng bình phương của chúng bằng 480.

Lời giải:

Gọi số hạng nhỏ nhất trong các số cần tìm là u và công sai của cấp số cộng là d.

Khi đó, năm số hạng liên tiếp là u, u + d, u + 2d, u + 3d, u + 4d.

Vì tổng của chúng bằng 40 nên u + u + d + u + 2d + u + 3d + u + 4d = 40

⇔ 5u + 10d = 40 ⇔ u + 2d = 8.

⇔ u = 8 – 2d. (1)

Lại có tổng bình phương của chúng bằng 480 nên

u² + (u + d)² + (u + 2d)² + (u + 3d)² + (u + 4d)² = 480. (2)

Thế (1) vào (2) ta được:

(8 – 2d)² + (8 – 2d + d)² + (8 – 2d + 2d)² + (8 – 2d + 3d)² + (8 – 2d + 4d)² = 480

⇔ (8 – 2d)² + (8 – d)² + 82 + (8 + d)² + (8 + 2d)² = 480

⇔ 64 – 32d + 4d² + 64 – 2d + d² + 64 + 64 + 2d + d² + 64 + 32d + 4d² = 480

⇔ 10d² + 320 = 480

⇔ 10d² = 160

⇔ d² = 16

⇔ d = ±4

+ Với d = 4, ta có u = 8 – 2 . 4 = 0.

+ Với d = – 4, ta có u = 8 – 2 . (– 4) = 16.

Vậy năm số hạng liên tiếp cần tìm là 0, 4, 8, 12, 16.

Bài 26 trang 51 SBT Toán 11 Tập 1: Cho (u_n) là cấp số cộng có u₁ + u₅ + u₉ + u₁₃ + u₁₇ + u₂₁ = 234.

a) Tính u₂ + u₈ + u₁₄ + u₂₀.

b) Tìm u₁, d, biết u₁₀ = 37.  

Lời giải:

a) Ta có: u₁ + u₅ + u₉ + u₁₃ + u₁₇ + u₂₁

= u₁ + (u₁ + 4d) + (u₁ + 8d) + (u₁ + 12d) + (u₁ + 16d) + (u₁ + 20d)

= 6u₁ + 60d

Mà u₁ + u₅ + u₉ + u₁₃ + u₁₇ + u₂₁ nên 6u₁ + 60d = 234 ⇔ u₁ + 10d = 39.

Lại có u₂ + u₈ + u₁₄ + u₂₀ = (u₁ + d) + (u₁ + 7d) + (u₁ + 13d) + (u₁ + 19d)

= 4u₁ + 40d = 4(u₁ + 10d) = 4 . 39 = 156. 

Vậy u₂ + u₈ + u₁₄ + u₂₀ = 156.

b) Ta có u₁ + 10d = (u₁ + 9d) + d = u₁₀ + d = 39.

Mà u₁₀ = 37 nên suy ra d = 39 – u₁₀ = 39 – 37 = 2.

Do đó, u₁ = 39 – 10d = 39 – 10 . 2 = 19.

Vậy u₁ = 19 và d = 2.

Bài 27 trang 51 SBT Toán 11 Tập 1: Cho dãy số (u_n) biết u₁ = – 2, u_n+1=$ \frac{u_{n}}{1-u_{n}}$ với n ∈ ℕ*. Đặt v_n= $ \frac{u_{n}+1}{u_{n}}$ với n ∈ ℕ*.

a) Chứng minh rằng dãy số (v_n) là một cấp số cộng. Tìm số hạng đầu, công sai của cấp số cộng đó.

b) Tìm công thức của v_n, u_n tính theo n.

c) Tính tổng S=$ \frac{1}{u_{1}}+\frac{1}{u_{2}}+\frac{1}{u_{3}}+...+\frac{1}{u_{20}}$

Lời giải:

a) Ta có v_n= $ \frac{u_{n}+1}{u_{n}}$ , v_n+1= $ 1+\frac{1}{u_{n+1}}=1+\frac{\frac{1}{u_{n}}}{1-u_{n}}=1+\frac{1-u_{n}}{u_{n}}=\frac{1}{u_{n}}$ Khi đó, v_n+1−v_n=$ \frac{1}{u_{n}}-(1+\frac{1}{u_{n}})=-1$ không đổi với mọi n ∈ ℕ*.

Vậy dãy số (v_n) là một cấp số cộng có số hạng đầu là v₁=và công sai d = – 1.

b) Ta có v_n=v₁+(n−1)d=$ \frac{1}{2}$+(n−1).(−1)=$ \frac{1}{2}$−n+1=$ \frac{3}{2}$−n

Vì v_n=$ 1+\frac{1}{u_{n}}$ nên $ 1+\frac{1}{u_{n}}$ = $ \frac{3}{2}-n$ ⇔$ \frac{1}{u_{n}}=\frac{1}{2}-n$ ⇔u_n=$ \frac{2}{1-2n}$

Vậy v_n=$ \frac{3}{2}$−n và u_n=$ \frac{2}{1-2n}$

c) Từ v_n=$1+\frac{1}{u_{n}}$ , suy ra $\frac{1}{u_{n}}=v_{n}-1$

Khi đó ta có S=$ \frac{1}{u_{1}}+\frac{1}{u_{2}}+\frac{1}{u_{3}}+...+\frac{1}{u_{20}}$

          = (v₁ – 1) + (v₂ – 1) + (v₃ – 1) + ... + (v₂₀ – 1)

          = (v₁ + v₂ + v₃ + ... + v₂₀) – 20.

Mà v₁ + v₂ + v₃ + ... + v₂₀ là tổng 20 số hạng đầu của cấp số cộng (v_n) nên

v₁ + v₂ + v₃ + ... + v₂₀= =-180

Do đó, S = – 180 – 20 = – 200.

Bài 28 trang 51 SBT Toán 11 Tập 1: Chuông đồng hồ ở một toà tháp đánh số tiếng đúng bằng số giờ và cứ mỗi 30 phút không phải là giờ đúng thì đánh 1 tiếng chuông. Hỏi bắt đầu từ lúc 1 giờ đêm đến 12 giờ trưa, chuông đồng hồ đó đã đánh tất cả bao nhiêu tiếng?

Lời giải:

Lúc 1 giờ đêm, toà tháp đánh 1 tiếng chuông; lúc 2 giờ đêm, toà tháp đánh 2 tiếng chuông, ...; lúc 12 giờ trưa, toà tháp đánh 12 tiếng chuông. Ngoài ra, mỗi 30 phút không phải là giờ đúng thì đánh 1 tiếng chuông (có 11 lần như thế từ 1 giờ đến 12 giờ).

Vậy tổng số tiếng chuông là:

S = (1 + 2 + 3 + ...+ 12) + 1 . 11 = $ \frac{(1+12).12}{2}+11$ = 89 (tiếng chuông).

Bài 29 trang 51 SBT Toán 11 Tập 1: Các khúc gỗ được xếp như Hình 2. Lượt thứ nhất có 21 khúc, lượt thứ hai có 20 khúc, ..., lượt trên cùng có 15 khúc. Tính tổng số khúc gỗ đã được xếp.

Lời giải:

Tổng số khúc gỗ được xếp là:

15 + 16 + ... + 21 = $ \frac{(15+21).7}{2}$ = 126 (khúc gỗ).