Bài 1 trang 94 SBT toán 11 tập 1: Cho hình chóp tứ giác S.ABCD có ABCD là hình bình hành. Điểm M thuộc cạnh SC. Trong các mặt phẳng sau, điểm M nằm trên mặt phẳng nào?

A. (ABCD)                       

B. (SAC)                

C. (SAB) 

D. (SAD)

Lời giải

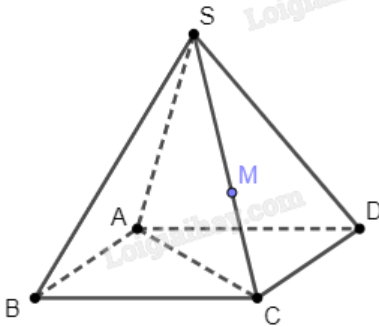
Theo hình vẽ, ta thấy SC nằm trong mặt (SAC).

Do M∈SC nên M nằm trên mặt phẳng (SAC)

Đáp án đúng là B.

Bài 2 trang 94 SBT toán 11 tập 1: Cho hình tứ diện ABCD. Giao tuyến của hai mặt phẳng (ABC) và (CDA) là đường thẳng:
A. AB                       

B. BD             

C. CD          

D. AC

Lời giải

Xét hai mặt phẳng (ABC) và (CDA) ta nhận thấy hai mặt phẳng này có hai điểm chung là A và C, do đó giao tuyến của hai mặt phẳng này là AC.

Đáp án đúng là D.

Bài 3 trang 94 SBT toán 11 tập 1: Một đồ vật trang trí có bốn mặt phân biệt là các tam giác (xem hình dưới đây). Vẽ hình hiểu diễn của đồ vật đó.
Lời giải

Do đồ vật trang trí có 4 mặt là các tam giác, nên nó có hình dạng một tứ diện.

Hình biểu diễn của nó như sau:

Bài 4 trang 94 SBT toán 11 tập 1: Cho tứ diện ABCD. Gọi M,N lần lượt là trung điểm của AB,CD. Chứng minh rằng bốn điểm M,N,C,D không cùng nằm trong một mặt phẳng.

Lời giải

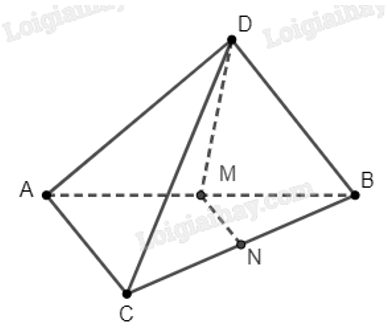
Do N là trung điểm của BC, nên 4 điểm B, N, C, D cùng nằm trong mặt phẳng.

Giả sử 4 điểm M, N, C, D cùng nằm trong một mặt phẳng.

Điều này có nghĩa là M∈(NCD).

Do bốn điểm B, N, C, D cùng nằm trong mặt phẳng, ta suy ra M∈(BCD).

Điểm M vàđiểm B cùng nằm trong mặt phẳng (BCD), nên BM⊂(BCD).

Mặt khác, do M là trung điểm của AB, nên A∈BM.

Suy ra A∈(BCD). Điều này là vô lí do ABCD là tứ diện nên bốn điểm A, B, C, D không cùng nằm trong một mặt phẳng.

Bài 5 trang 95 SBT toán 11 tập 1: Cho hai mặt phẳng (P),(Q) cắt nhau theo giao tuyến d và hai đường thẳng a,b lần lượt nằm trong (P),(Q). Chứng minh rằng nếu hai đường thẳng a,b cắt nhau thì giao điểm của chúng thuộc đường thẳng d.

Lời giải

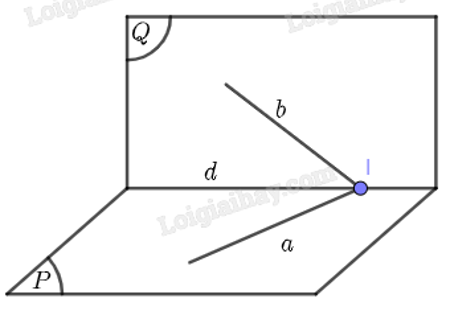
Gọi I là giao điểm của hai đường thẳng a và b. Suy ra I∈a và I∈b

Vì a⊂(P) và b⊂(Q), ta suy ra I∈(P) và I∈(Q), tức là I thuộc giao tuyến của hai mặt phẳng (P) và (Q). Mà (P)∩(Q)=d, suy ra I∈d.

Bài toán được chứng minh.

Bài 6 trang 95 SBT toán 11 tập 1: Cho tứ diện ABCD. Trên các cạnh AC,CD lần lượt lấy các điểm E,F sao cho CE=3EA,DF=2FC.

a)    Xác định giao tuyến của mặt phẳng (BEF) với các mặt phẳng (ABC), (ACD), (BCD).

b)    Xác định giao điểm K của đường thẳng AD với mặt phẳng (BEF).

c)     Xác định giao tuyến của hai mặt phẳng (BEF) và (ABD).

Lời giải
a)

Giao tuyến của (BEF) và (ABC):

Ta có B∈(BEF)∩(ABC)

Mặt khác, ta có E∈(BEF) và E∈AC⊂(ABC)⇒E∈(BEF)∩(ABC)

Như vậy giao tuyến của (BEF) và (ABC) là đường thẳng BE.

Giao tuyến của (BEF) và (ACD):

Ta có F∈(BEF) và F∈CD⊂(ACD)⇒F∈(BEF)∩(ACD

Mặt khác, E∈(BEF) và E∈AC⊂(ACD)⇒E∈(BEF)∩(ACD

Như vậy giao tuyển của (BEF) và (ACD) là đường thẳng EF.

Giao tuyến của (BEF) và (BCD):

Ta có B∈(BEF)∩(BCD)

Mặt khác, F∈(BEF) và F∈CD⊂(BCD)⇒F∈(BEF)∩(BCD)

Như vậy giao tuyển của (BEF) và (BCD) là đường thẳng BF.

b) Trên mặt phẳng (ACD), lấy K là giao điểm của AD và EF.

Ta có {K}=AD∩EF,  mà EF⊂(BEF).

Suy ra {K}=AD∩(BEF), tức K là giao điểm của AD và (BEF).

c) Ta có B∈(BEF)∩(ABD).

Theo câu b, ta có K∈AD∩(BEF)⇒K∈AD và K∈(BEF) Mà AD∈(ABD) nên ta suy ra K∈(ABD) và K∈(BEF)⇒K∈(ABD)∩(BEF

Vậy giao tuyến của hai mặt phẳng (BEF) và (ABD) là đường thẳng BK.

Bài 7 trang 95 SBT toán 11 tập 1: Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M,N,P lần lượt là trung điểm của các cạnh SA,BC,CD

a)    Xác định giao điểm của đường thẳng NP với mặt phẳng (SAB)

b)    Xác định giao tuyến của mặt phẳng (MNP) với các mặt phẳng (SAB),(SAD),(SBC),(SCD)

Lời giải

a) Xét mặt phẳng (ABCD), gọi E là giao điểm của AB và NP.

Ta có {E}=AB∩NP, mà NP⊂(MNP) nên {E}=(SAB)∩NP.

b)

Giao tuyến của (MNP) và (SAB):

Ta có M∈SA⊂(SAB) và M∈(MNP)⇒M∈(SAB)∩(MNP.

Mặt khác, theo câu a, ta có E∈AB⊂(SAB) và E∈NP⊂(MNP)⇒E∈(SAB)∩(MNP)

Từ đó, giao tuyến của hai mặt phẳng (SAB) và (MNP) là đường thẳng ME.

Giao tuyến của (MNP) và (SAD):

Trên mặt phẳng (ABCD) gọi F là giao điểm của AD và NP.

Vì F là giao điểm của AD và NP, ta suy ra F∈AD và F∈NP

Do AD⊂(SAD), NP⊂(MNP) nên ta có F∈(SAD) và F∈(MNP)⇒F∈(SAD)∩(MNP

Hơn nữa, ta cũng có M∈SA⊂(SAD) và M∈(MNP)⇒M∈(SAD)∩(MNP

Vậy giao tuyến của hai mặt phẳng (SAD) và (MNP) là đường thẳng MF.

Giao tuyến của (MNP) và (SBC):

Ta có ME là giao tuyến của hai mặt phẳng (SAB) và (MNP)⇒ME⊂(SAB)

Trên mặt phẳng (SAB), gọi {K}=ME∩SB.

Suy ra K∈ME⊂(MNP) và K∈SB⊂(SBC)⇒K∈(MNP)∩(SBC)

Hơn nữa, ta có N∈(MNP) và N∈BC⊂(SBC)⇒N∈(MNP)∩(SBC)

Vậy giao tuyến của hai mặt phẳng (SBC) và (MNP) là đường thẳng NK.

Giao tuyến của (MNP) và (SCD):

Ta có MF là giao tuyến của hai mặt phẳng (SAD) và (MNP)⇒MF⊂(SAD)

Trên mặt phẳng (SAD), gọi {L}=MF∩SD.

Suy ra L∈MF⊂(MNP) và L∈SD⊂(SCD)⇒L∈(MNP)∩(SCD)

Hơn nữa, ta có P∈(MNP) và P∈CD⊂(SCD)⇒P∈(MNP)∩(SCD)

Vậy giao tuyến của hai mặt phẳng (SCD) và (MNP) là đường thẳng LP.

Bài 8 trang 95 SBT toán 11 tập 1: Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M,N,P lần lượt là trung điểm của các cạnh SA,SB,SC.

a)    Xác định giao điểm I của đường thẳng MP với mặt phẳng (SBD)

b)    Xác định giao điểm Q của đường thẳng SD với mặt phẳng (MNP).
Lời giải

a) Trên mặt phẳng (ABCD), gọi {O}=AC∩BD.

Trên mặt phẳng (SAC), gọi {I}=MP∩SO.

Do SO⊂(SBD) ta suy ra {I}=MP∩(SBD)

Vậy I là giao điểm của MP và (SBD).

b) Trên mặt phẳng (SBD), gọi {Q}=NI∩SD.

Do NI⊂(MNP) ta suy ra {Q}=(MNP)∩SD.

Vậy Q là giao điểm của SD và (MNP).

Bài 9 trang 95 SBT toán 11 tập 1: Cho hình chóp tứ giác S.ABCD có đáy không là hình thang. Gọi O là giao điểm của AC và BD. Trên SO lấy điểm I sao cho SI=2IO.

a) Xác định các giao điểm M, N lần lượt của SA, SD với mặt phẳng (IBC).

b*) Chứng minh rằng các đường thẳng AD, BC và MN đồng quy.

Lời giải

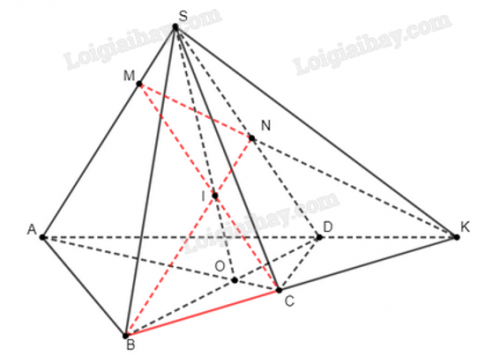
a)

Giao điểm M của SA và (IBC):

Ta nhận xét rằng I∈SO⊂(SAC)⇒CI⊂(SAC)

Trên mặt phẳng (SAC), gọi {M}=CI∩SA.

Do IC⊂(IBC), nên {M}=(IBC)∩SA.

Vậy M là giao điểm của (IBC) và SA.

Giao điểm N của SD và (IBC):

Ta nhận xét rằng I∈SO⊂(SBD)⇒BI⊂(SBD).

Trên mặt phẳng (SBD), gọi {N}=BI∩SD.

Do IB⊂(IBC), nên {N}=(IBC)∩SD.

Vậy N là giao điểm của (IBC) và SD.

b) Trên mặt phẳng (ABCD), gọi K là giao điểm của AD và BC.

Ta có M∈SA⊂(SAD) và M∈(IBC)⇒M∈(SAD)∩(IBC)

Mặt khác, N∈SD⊂(SAD) và N∈(IBC)⇒N∈(SAD)∩(IBC).

Vậy giao tuyến của (SAD) và (IBC) là đường thẳng MN.

Do AD∈(SAD), BC∈(IBC), {K}=AD∩BC, ta suy ra K nằm trên giao tuyến của (SAD) và (IBC), tức là K∈MN.

Vậy ba đường thẳng AD, BC, MN cắt nhau tại K.