BÀI 2: HÌNH CHỮ NHẬT – HÌNH THOI

HÌNH BÌNH HÀNH – HÌNH THANG CÂN 

1. Hình chữ nhật

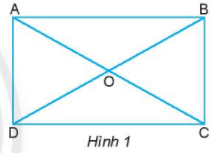
Bài 1: Cho hình chữ nhật ABCD (Hình 1).

a) Đo rồi so sánh các cạnh và góc của hình chữ nhật.

b) Hãy kiểm tra xem hai cặp cạnh AB và CD, BC và AD có song song với nhau không.

c) AC và BD được gọi là hai đường chéo của hình chữ nhật. Hãy đo rồi so sánh AC và BD.

Giải nhanh:

a) - Các góc bằng nhau.

- AB = CD, AD = BC

b) AB // CD, BC // AD 

c) AD = BD 

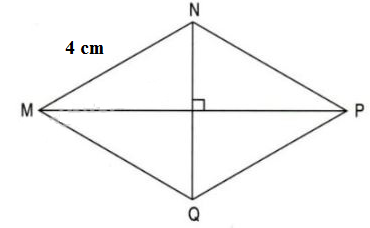
Bài 2: Đo và so sánh độ dài các đoạn OM, ON, OP và OQ của hình chữ nhật MNPQ.

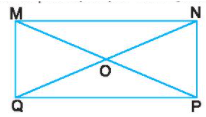
Giải nhanh:

OM = ON = OP = OQ

Bài 3: Sắp xếp các Hình 3a, b, c thành hình chữ nhật sao cho sau khi được sắp xếp tạo thành bức tranh như hình 3d.

Giải nhanh:

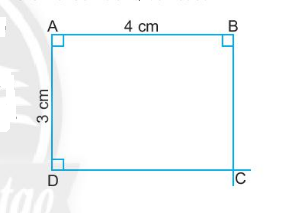
Bài 4: Vẽ hình chữ nhật ABCD có AB = 4 cm, AD = 3 cm theo hướng dẫn sau:

- Vẽ đoạn thẳng AB = 4 cm và đoạn thẳng AD = 3 cm vuông góc với nhau.

- Qua B vẽ đường thẳng vuông góc với AB.

- Qua D vẽ đường thẳng vuông góc với AD.

Giải nhanh:

Bài 5: Hãy xếp và cắt một tờ giấy hình chữ nhật thành bốn hình chữ nhật có cùng chiều dài và chiều rộng.

Giải nhanh:

• Bước 1: Ta xếp đôi 2 lần hình chữ nhật.

• Bước 2: Mở hình chữ nhật đã xếp ra.

• Bước 3: Dùng kéo cắt theo đường của các nếp gấp để thành 4 hình chữ nhật có cùng chiều dài và chiều rộng.

2. Hình thoi

Bài 1: Cho hình thoi ABCD như hình 4.

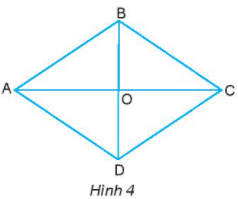
a) Hãy so sánh các cạnh của hình thoi.

b) Hãy kiểm tra xem hai cặp cạnh AB và CD, BC và AD có song song với nhau không.

c) AC và BD được gọi là hai đường chéo của hình thoi. Dùng eke để kiểm tra xem hai đường chéo có vuông góc với nhau hay không.

Giải nhanh:

a) AB = BC = CD = DA

b) AB // CD, BC // AD 

c) AC và BD vuông góc với nhau.

Bài 2: Cho hình thoi IJKL, hai đường chéo cắt nhau tại O (Hình 6).

- Dùng eke để kiểm tra xem hai đường chéo có vuông góc với nhau hay không.

- Dùng compa để kiểm tra hai đường chéo có cắt nhau tại trung điểm của mỗi đường hay không.

Giải nhanh:

- LJ, IK vuông góc với nhau.

- LJ, IK cắt nhau tại trung điểm mỗi đường.

Bài 3: Vẽ hình thoi ABCD khi biết AB = 3 cm và đường chéo AC = 5 cm theo hướng dẫn sau:

- Vẽ đoạn thẳng AC = 5 cm.

- Lấy A và C làm tâm, vẽ hai đường tròn bán kính 3 cm (hình vẽ), hai đường tròn này cắt nhau tại điểm B và D.

- Nối B với A, B với C, D với A, D với C.

ABCD là hình thoi cần vẽ.

Giải nhanh:

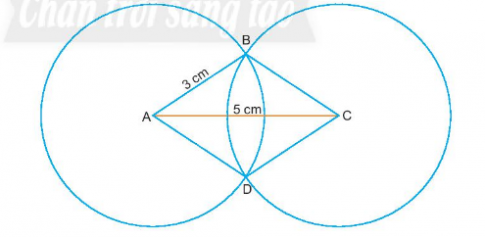
Bài 4: Vẽ hình thoi MNPQ biết cạnh MN = 4 cm. Em hãy thảo luận với các bạn về các hình vừa vẽ.

Giải nhanh:

Hình thoi có MNPQ có các cạnh bằng nhau, các đường chéo vuông góc nhau và cắt nhau tại trung điểm hai đường.

3. Hình bình hành

Bài 1: Cho hình bình hành ABCD như Hình 7.

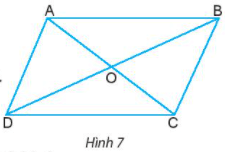
a) Hãy đo rồi so sánh cạnh AB và CD; cạnh BC và AD.

b) Hãy kiểm tra xem các cặp cạnh AB và CD, BC và AD có song song với nhau không.

c) AC và BD được gọi là hai đường chéo của hình bình hành.

Hai đường chéo AC và BD cắt nhau tại O. Hãy so sánh OA và OC; OB và OD.

Giải nhanh:

a) AB = CD, AD = BC

b) AB // CD và AD // BC

c) OA = OC, OB = OD

Bài 2: Quan sát hình bình hành bên và cho biết

- Góc đỉnh M của hình bình hành MNPQ bằng góc nào?

- OM, ON lần lượt bằng những đoạn nào?

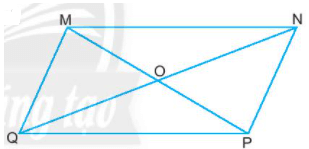
Giải nhanh:

- Góc ở đỉnh M = góc ở đỉnh P

- OM = OP, OM = OQ

Bài 3: Bác Lê muốn ghép 3 tấm ván như hình vẽ bên thành một mặt bàn hình bình hành. Em hãy giúp bác Lê thực hiện việc này nhé!

Giải nhanh:

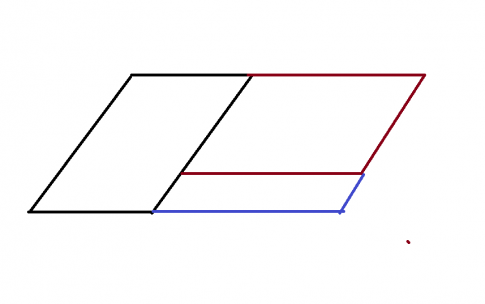
Bài 4: Vẽ hình bình hành ABCD khi biết AB = 3 cm, BC = 5 cm và đường chéo AC = 7 cm theo hướng dẫn sau:

Giải nhanh:

AB = CD, BC = AD

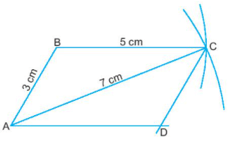
Bài 5: Vẽ hình bình hành ABCD khi biết hai đường chéo AC = 5 cm, BD = 7 cm. Em hãy thảo luận với bạn về các hình đã vẽ.

Giải nhanh:

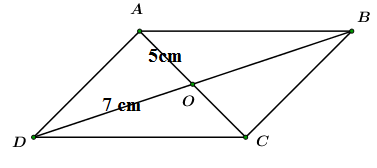
Thảo luận:

- AB = CD, BC = AD

- AC Và DB cắt nhau tại tâm O

- AB // CD, BC // AD

4. Hình thang cân

Bài 1: Cho hình thang cân như Hình 9.

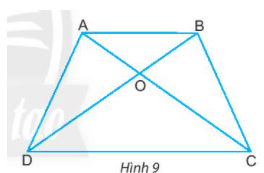
a) Hãy đo rồi so sánh hai cạnh bên BC và AD. 

b) Hãy kiểm tra xem AB có song song với CD hay không.

c) AC và BD được gọi là hai đường chéo. Hãy đo rồi so sánh AC và BD.

Giải nhanh:

a) BC = AD

b) AB // CD.

c) AC = BD

Bài 2: Cho hình thang cân như hình bên.

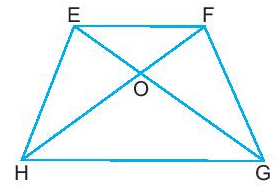
Hãy cho biết:

- Góc ở đỉnh H của hình thang cân EFGH là bằng góc nào?

- EG, EH lần lượt bằng các đoạn thẳng nào?

Giải nhanh:

- Góc đỉnh H = góc đỉnh G.

- EG = FH và EH = FG.

Bài 3: Gấp đôi một tờ giấy hình chữ nhật, rồi cắt theo đường nét đứt như hình bên dưới, sau đó trải tờ giấy ra. Hình vừa cắt ra được hình gì?

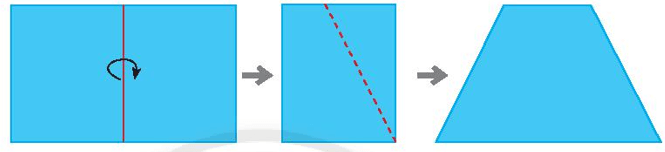
Giải nhanh:

5. Bài tập

Bài 1: Trong các hình sau đây hình nào là hình chữ nhật, hình bình hành, hình thoi, hình thang cân?

Giải nhanh:

• Hình thoi

• Hình thang cân

• Hình chữ nhật

• Hình bình hành

Bài 2: Đo rồi cho biết độ dài các cạnh của mỗi hình chữ nhật sau:

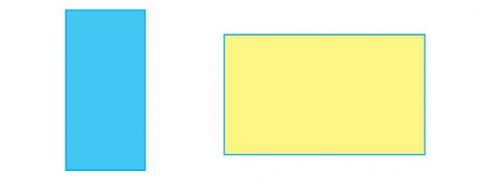
Giải nhanh:

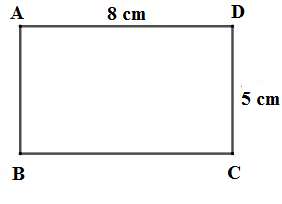
Bài 3: Vẽ hình chữ nhật ABCD biết AB = 5 cm, AD = 8 cm.

Giải nhanh:

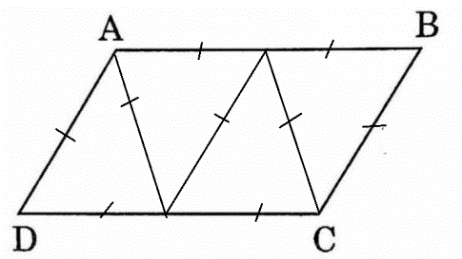
Bài 4: Người ta có thể thiết kế một mặt bàn hình bình hành bằng cách ghép bon miếng gỗ hình tam giác đều lại với nhau. Để biết được cách thiết kế như thế nào, hãy cắt 4 hình tam giác đều cạnh 5 cm, rồi ghép thành một hình bình hành.

Giải nhanh:

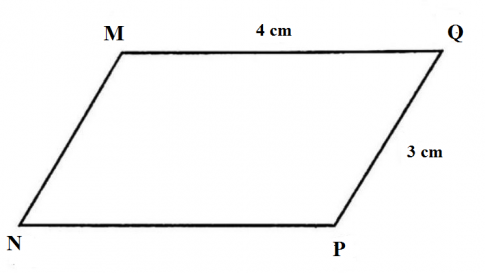
Bài 5: Vẽ hình bình hành MNPQ biết: MN = 3 cm, NP = 4 cm.

Giải nhanh:

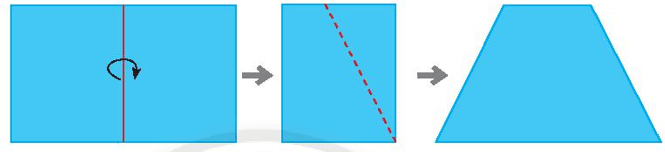
Bài 6: Lấy một tờ giấy hình chữ nhật, gấp đôi hai lần, cắt theo đường nét đứt như hình dưới, rồi trải tờ giấy ra. Hinh vừa cắt được là hình gì? Dùng êke để kiểm tra hai đường chéo của hình cắt được có vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường hay không.

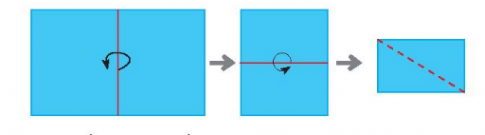
Giải nhanh:

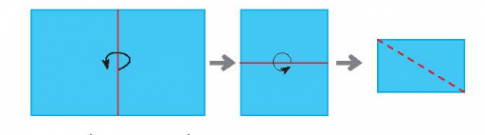
Hai đường chéo của hình vừa cắt được vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.

Bài 7: Vẽ hình thoi MNPQ biết góc MNP bằng 60° và MN = 6 cm.

Giải nhanh:

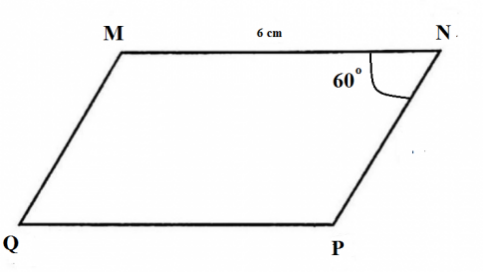
Bài 8: Cắt ba hình tam giác đều cạnh 4 cm rồi ghép lại thành một hình thang cân.

Giải nhanh:

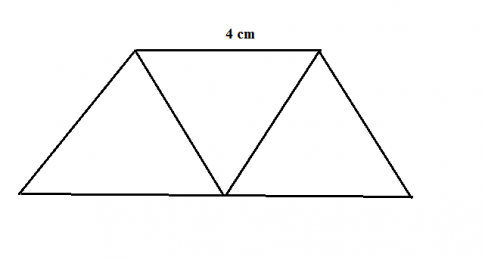
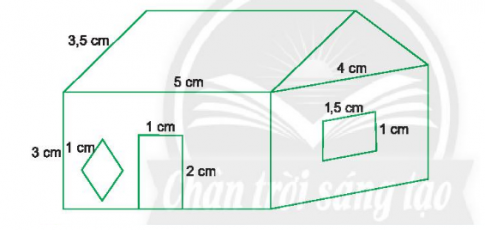
Bài 9: Vẽ sơ đồ ngôi nhà theo kích thước các cạnh nêu ra trong hình vẽ dưới đây.

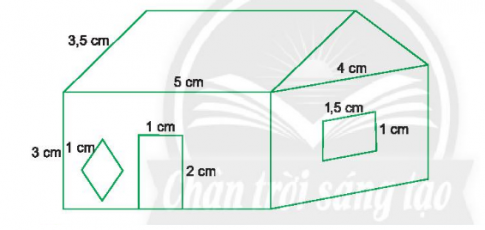
Giải nhanh: