A. KIẾN THỨC TRỌNG TÂM

1. PHẦN ĐẠI SỐ

Chương VI: Phân số

- So sánh hai phân số: 

• Cùng mẫu: Trong hai phân số cùng một mẫu dương, phân số nào có tử lớn hơn thì phân số đó lớn hơn.
• Không cùng mẫu: viết chúng dưới dạng hai phân số có cùng một mẫu dương rồi so sánh các tử số với nhau: phân số nào có tử số lớn hơn thì phân số đó lớn hơn.

- Hỗn số dương: Với a, b, c là những số nguyên dương, ta gọi $a\frac{b}{c}$ là một hỗn số dương với a là phần nguyên và $\frac{b}{c}$ là phần phân số. 

- Phép cộng phân số:

• Cùng mẫu $\frac{a}{m}+\frac{b}{m}=\frac{a+b}{m}$ với $a,b,m\in \mathbb{Z};m\neq0$
• Không cùng mẫu: viết chúng dưới dạng hai phân số cùng mẫu rồi cộng các tử và giữ nguyên mẫu.
• Số đối: $\frac{a}{b}+(-\frac{a}{b})=0$ với $a,b\in \mathbb{Z};b\neq0$

- Phép trừ phân số: 

• Cùng mẫu $\frac{a}{n}-\frac{b}{m}=\frac{a-b}{m}$ với $a,b,m\in \mathbb{Z};m\neq0$
• Không cùng mẫu: ta quy đồng mẫu hai phân số rồi trừ hai phân số đó.

- Phép nhân phân số: Cho $a, b, c, d ∈ ℤ; b≠0; d≠0.$ Khi đó phép nhân hai phân số ta có: $\frac{a}{b}.\frac{c}{d}=\frac{a.c}{b.d}$

- Phép chia phân số:

• $\frac{a}{b}:\frac{c}{d}=\frac{a}{b}.\frac{d}{c}=\frac{ad}{bc}$ với $a,b,c,d \in \mathbb{Z};a, b, c,\neq0$
• $\frac{a}{b}:\frac{b}{a}=1$ khi đó phân số $\frac{b}{a}$ là nghịch đảo của $\frac{a}{b}$ Cho $a, b ∈ ℤ; a, b ≠ 0$

Chương VII: Số thập phân

- Phép cộng số thập phân:

• Cộng hai số thập phân âm $(–a) + (–b) = – (a + b)$ với $a, b > 0$
• Cộng hai số thập phân khác dấu 

+ Nếu $0 < a b$ thì$ (–a) + b = b – a$

+ Nếu $a > b > 0$ thì$ (–a) + b = –(a – b)$

- Phép trừ số thập phân: đưa về phép cộng hai số đối $a – b  = a + (–b)$

- Phép nhân số thập phân: 

• Nhân hai số cùng dấu: $(–a).(–b) = a.b$  với $a, b > 0$

• Nhân hai số khác dấu: $(–a).b = a.(–b) = – (a.b)$với $a, b > 0$

- Phép chia số thập phân: 

• Chia hai số nguyên cùng dấu: $(–a) : (–b) = a : b$ với $a, b > 0$

• Chia hai số nguyên khác dấu: $(–a) : b = a : (–b) = –(a:b)$ với $, b > 0$

- Làm tròn số thập phân: 

• Nếu chữ số bên phải hàng quy tròn lớn hơn hoặc bằng 5 thì tăng chữ số hàng quy tròn lên một đơn vị rồi thay tất cả các chữ số bên phải bằng số 0 hoặc bỏ đi nếu chúng ở phần thập phân
• Nếu chữ số bên phải hàng quy tròn nhỏ hơn hoặc bằng 5 thì giảm chữ số hàng quy tròn lên một đơn vị rồi thay tất cả các chữ số bên phải bằng số 0 hoặc bỏ đi nếu chúng ở phần thập phân

- Tỉ số: tỉ số của a và b kí hiệu là $a : b$ hoặc $\frac{a}{b}$

- Tỉ số phần trăm của a và b là $\frac{a}{b}.100%$

- Ứng dụng tỉ số phần trăm:

Muốn tìm giá trị m% của số a, ta tính $a\frac{m}{100}$

Muốn tìm một số khi biết m% của số đó bằng b ta tính $b:\frac{m}{100}$

Chương IX: Dữ liệu và xác suất thực nghiệm

- Biểu đồ cột là một loại biểu đồ được dùng trong thống kê, thường được dùng để thể hiện thay cho biểu đồ tranh khi số liệu thống kê là những số liệu lớn, phức tạp, hoặc số liệu có số thập phân.

Vẽ biểu đồ 

• Bước 1: Vẽ 2 trục ngang và dọc vuông góc với nhau

+ Trục ngang ghi danh sách đối tượng

+ Trục dọc chọn khoảng cách chia thích hợp với dữ liệu và ghi ở các vạch chia.

• Bước 2: Tại vị trí các đối tượng trên trục ngang, vẽ các cột hình chữ nhật

+ Cách đều nhau

+ Có cùng chiều rộng

+ Có chiều cao thể hiện số liệu của các đối tượng, tương ứng với khoảng chia trên trục dọc.

• Bước 3: Hoàn thiện biểu đồ

+ Ghi tên biểu đồ

- Biểu đồ cột kép được tạo thành khi ghép hai biểu đồ cột lại với nhau.

2. PHẦN HÌNH HỌC

Chương VIII: Những hình học cơ bản

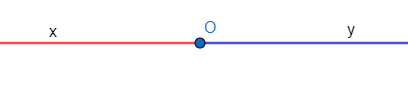
- Một phần đường thẳng bị chia ra bởi điểm O được gọi là một tia gốc O

- Hai tia Ox và Oy là gọi là hai tia đối nhau

- Hai tia trùng nhau là hai tia chung gốc và có thêm ít nhất 1 điểm chung khác điểm gốc

- I nằm giữa hai điểm A và B sao cho IA = IB thì I gọi là trung điểm của đoạn thẳng AB. $IA=IB=\frac{AB}{2}$

-Góc là hình gồm hai tia chung gốc. Gốc chung của hai tia gọi là đỉnh của góc. Hai tia là hai cạnh của góc.

- Mỗi góc có một số đo. Số đo của một góc không vượt quá $180^{\circ}$.

- Góc đặc biệt:

• Góc có số đo bằng $90^{\circ}$ là góc vuông.

• Góc bẹt là góc có số đo bằng $180^{\circ}$.
• Góc nhỏ hơn góc vuông là góc nhọn.
• Góc lớn hơn góc vuông và nhỏ hơn góc bẹt là góc tù.