BÀI 1. PHƯƠNG TRÌNH MẶT PHẲNG

1. Vecto pháp tuyến và cặp vectơ chỉ phương của mặt phẳng

HĐ1:

a) Cho vectơ khác . Qua một điểm , cố định trong không gian, có bao nhiêu mặt phẳng vuông góc với giá của vectơ ?

b) Cho hai vectơ , không cùng phương. Qua một điểm , cố định trong không gian, có bao nhiêu mặt phẳng song song hoặc chứa giá của hai vectơ , ?

Đáp án chuẩn:

a) Chỉ có một mặt phẳng  

b) Chỉ có một mặt phẳng  

TH1: Trong không gian , cho ba điểm .

a) Tìm toạ độ của một cặp vectơ chỉ phương của mặt phẳng .

b) Tìm tọa độ của một vectơ pháp tuyến của mặt phẳng .

Đáp án chuẩn:

a) và

b) .

Vận dụng 1: Một lăng kính có dạng hình lăng trụ đứng có đáy là tam giác đều ở Hình 3a được vẽ lại như Hình 3b. Tìm một cặp vectơ chỉ phương và một vectơ pháp tuyến của mặt phẳng .

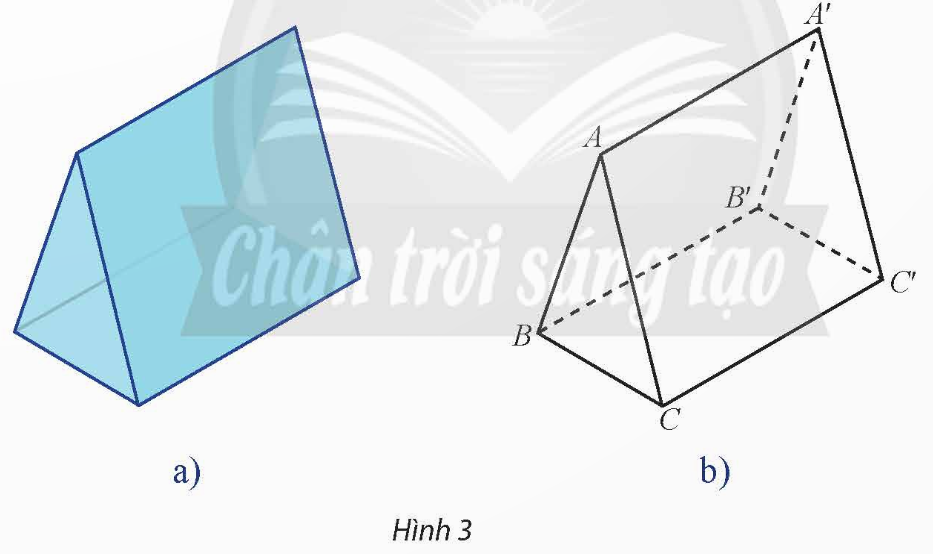
Đáp án chuẩn:

, là một cặp vectơ chỉ phương của

là một vectơ pháp tuyến của mặt phẳng

2. Xác định vectơ pháp tuyến của mặt phẳng khi biết một cặp vectơ chỉ phương

HĐ2: Trong không gian Oxyz, cho mặt phẳng có cặp vectơ chỉ phương , . Xét vectơ

a) Vectơ khác vecto hay không?

b) Tính ; .

c) Vecto có phải là vectơ pháp tuyến của mặt phẳng hay không?

Đáp án chuẩn:

a) .

b) ;   

c) là vectơ pháp tuyến của mặt phẳng

TH2: Cho mặt phẳng đi qua ba điểm , , . Tìm một cặp vectơ chỉ phương và một vectơ pháp tuyến của .

Đáp án chuẩn:

Mặt phẳng nhận làm một vectơ pháp tuyến

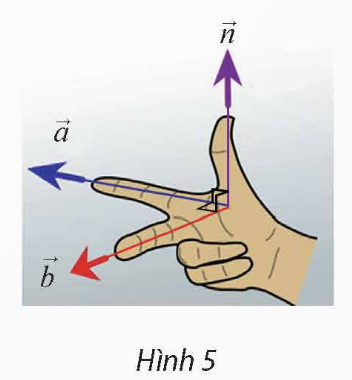
Vận dụng 2: Cho biết hai vectơ , có giá lần lượt song song với ngón trỏ và ngón giữa của bàn tay trong Hình 5. Tìm vectơ có giá song song với ngón cái. (Xem như ba ngón tay nói trên tạo thành ba đường thẳng đôi một vuông góc.)

Đáp án chuẩn:

3. Phương trình tổng quát của mặt phẳng. 

Khái niệm phương trình tổng quát của mặt phẳng

HĐ3: Trong không gian , cho mặt phẳng đi qua điểm và nhận làm vectơ pháp tuyến. Gọi là một điểm tùy ý trong không gian. Tính tích vô hướng theo .

Đáp án chuẩn:

TH3: Cho hai mặt phẳng có phương trình tổng quát là

và .

a) Tìm một vectơ pháp tuyến của mỗi mặt phẳng

b) Tìm điểm thuộc mặt phẳng trong số các điểm: , .

Đáp án chuẩn:

a) Mặt phẳng có một vectơ pháp tuyến là

Mặt phẳng có một vectơ pháp tuyến là

b) thuộc  

Lập phương trình tổng quát của mặt phẳng đi qua một điểm và biết vectơ pháp tuyến

HĐ4: Trong không gian , cho mặt phẳng đi qua điểm và nhận làm vectơ pháp tuyến. Gọi là một điểm tùy ý trong không gian.

a) Tìm toạ độ của .

b) Tính tích vô hướng .

c) Lập phương trình tổng quát của mặt phẳng .

Đáp án chuẩn:

a)

b)

c) 

Lập phương trình tổng quát của mặt phẳng đi qua một điểm và biết cặp vectơ chỉ phương

HĐ5: Trong không gian , cho mặt phẳng đi qua điểm và có cặp vectơ chỉ phương là , .

a) Tìm toạ độ một vectơ pháp tuyến của mặt phẳng .

b) Lập phương trình của mặt phẳng .

Đáp án chuẩn:

a)

b)

Lập phương trình tổng quát của mặt phẳng đi qua ba điểm không thẳng hàng

HĐ6: Trong không gian , cho mặt phẳng đi qua ba điểm , , .

a) Tìm toạ độ một cặp vectơ chỉ phương của mặt phẳng .

b) Tìm tọa độ một vectơ pháp tuyến của mặt phẳng .

c) Lập phương trình của mặt phẳng .

Đáp án chuẩn:

a) và , 

b)

c)

TH4: Viết phương trình mặt phẳng trong mỗi trường hợp sau:

a) đi qua điểm và có vectơ pháp tuyến .

b) đi qua điểm và có cặp vectơ chỉ phương là , .

c) đi qua ba điểm . 

d) đi qua ba điểm .

Đáp án chuẩn:

a)

b)

c)

d)

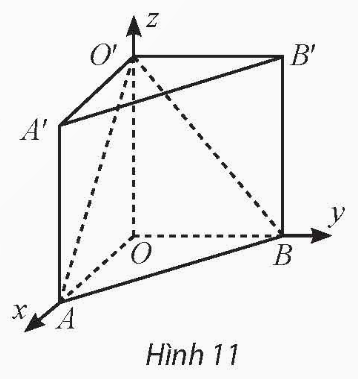
Vận dụng 3: Trong không gian Oxyz, cho hình lăng trụ . Biết là gốc toạ độ, , , . Viết phương trình các mặt phẳng và .

Đáp án chuẩn:

4. Điều kiện để hai mặt phẳng song song, vuông góc

Điều kiện để hai mặt phẳng song song

HĐ7: Cho hai mặt phẳng có phương trình là

và .

a) Nêu nhận xét về các vectơ pháp tuyến của hai mặt phẳng trên.

b) Cho điểm . Hãy cho biết các mặt phẳng có đi qua không. 

c) Giải thích tại sao song song với .

Đáp án chuẩn:

a) 2 vecto và cùng phương

b) thuộc ; không thuộc  

c) Vì và tương ứng là vectơ pháp tuyến của hai mặt phẳng và cùng phương với nhau nên song song hoặc trùng nhau

Tuy nhiên điểm và nên không trùng nhau 

=> song song với .

TH5: Mặt phẳng song song với mặt phẳng nào sau đây?

a) ;

b) ;

c) .

Đáp án chuẩn:

Vận dụng 4: Trên bản thiết kế đồ hoạ 3D của một cánh đồng điện mặt trời trong không gian , một tấm pin nằm trên mặt phẳng ; một tấm pin khác nằm trên mặt phẳng đi qua điểm và song song với Viết phương trình mặt phẳng .

Đáp án chuẩn:

Điều kiện để hai mặt phẳng vuông góc

HĐ8: Cho hai mặt phẳng có phương trình là

và .

a) Chỉ ra hai vectơ , lần lượt là vectơ pháp tuyến của . 

b) Tính tích vô hướng và nêu nhận xét về hai mặt phẳng . 

Đáp án chuẩn:

a) có vectơ pháp tuyến

có vectơ pháp tuyến

b)  ;

TH6: Tìm các cặp mặt phẳng vuông góc trong các mặt phẳng sau:

,

,

.

Đáp án chuẩn:

 ;  

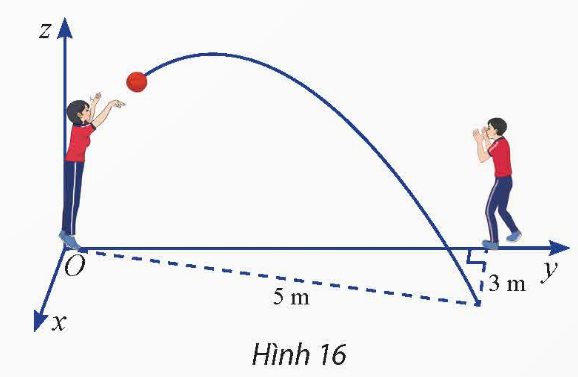
Vận dụng 5: Hai học sinh đang chuyền bóng. Bạn nữ ném bóng cho bạn nam. Quả bóng bay trên không, lệch sang phải và rơi xuống tại vị trí cách bạn nam 3 m, cách bạn nữ 5m (Hình 16). Cho biết quỹ đạo của quả bóng nằm trong mặt phẳng vuông góc với mặt đất. Hãy viết phương trình của trong không gian được mô tả như trong hình vẽ.

Đáp án chuẩn:

hương trình của là:

5. Khoảng cách từ một điểm đến một mặt phẳng

HĐ9: Trong không gian , cho mặt phẳng có phương trình và điểm . Gọi là hình chiếu vuông góc của trên (Hình 17).

a) Nêu nhận xét về phương của hai vectơ: 

và . 

b) Tính theo và toạ độ của .

c) Giải thích tại sao ta lại có đẳng thức .

d) Từ các kết quả trên suy ra cách tính .

Đáp án chuẩn:

a) 2 vecto và cùng phương

b)

c) .

d)

TH7:  

 a) Tính chiều cao của hình chóp với toạ độ các đỉnh là , , , .

b) Tính khoảng cách giữa hai mặt phẳng song song và .

Đáp án chuẩn:

a) 

b)

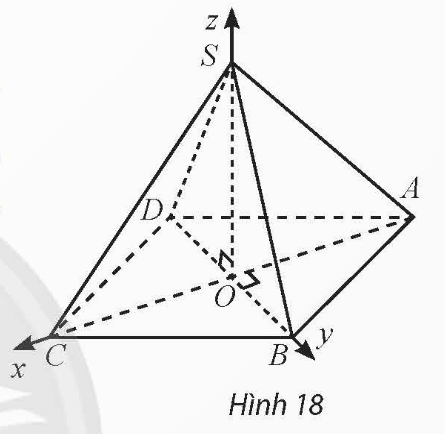
Vận dụng 6: Cho hình chóp tứ giác đều có cạnh đáy bằng , chiều cao bằng và là tâm của đáy. Bằng cách thiết lập hệ trục toạ độ như Hình 18, tính khoảng cách từ điểm đến mặt phẳng .

Đáp án chuẩn:

GIẢI BÀI TẬP

Bài 1: Viết phương trình của mặt phẳng:

a) Đi qua điểm và nhận làm vectơ pháp tuyến;

b) Đi qua điểm và song song với giá của mỗi vectơ và ; 

c) Đi qua ba điểm , và .

Đáp án chuẩn:

a)

b)

c)

Bài 2: 

a) Lập phương trình của các mặt phẳng toạ độ , , .

b) Lập phương trình của các mặt phẳng đi qua điểm và lần lượt song song với các mặt phẳng tọa độ trên.

Đáp án chuẩn:

a) Mặt phẳng :

Mặt phẳng :

Mặt phẳng :

b) Mặt phẳng song song với mặt phẳng nên có dạng:

Mặt phẳng song song với mặt phẳng nên có dạng:

Mặt phẳng song song với mặt phẳng nên có dạng:

Bài 3: Cho tứ diện có các đỉnh , , , .

a) Hãy viết phương trình của các mặt phẳng và .

b) Hãy viết phương trình mặt phẳng đi qua cạnh và song song với cạnh .

Đáp án chuẩn:

a) Phương trình của là:

Phương trình của là:

b) Phương trình của là:

Bài 4: Viết phương trình mặt phẳng đi qua điểm và song song với mặt phẳng .

Đáp án chuẩn:

Bài 5: Viết phương trình mặt phẳng đi qua hai điểm , và vuông góc với mặt phẳng .

Đáp án chuẩn:

Phương trình của là:

Bài 6: Viết phương trình mặt phẳng đi qua điểm và vuông góc với hai mặt phẳng , .

Đáp án chuẩn:

Phương trình của là:

Bài 7: Tính khoảng cách từ gốc tọa độ và từ điểm đến mặt phẳng

Đáp án chuẩn:

;

Bài 8: Tính khoảng cách giữa hai mặt phẳng song song và .

Đáp án chuẩn:

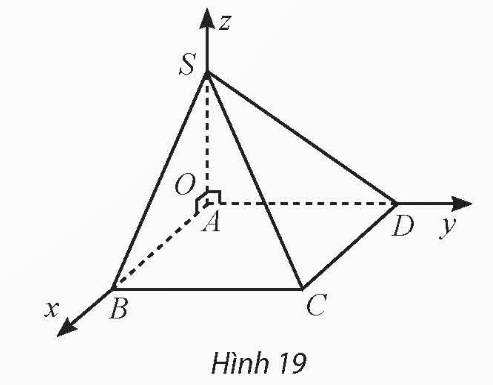
Bài 9: Cho hình chóp có đáy là hình chữ nhật với , , và . Bằng cách thiết lập hệ trục toạ độ như Hình 19, tính khoảng cách từ điểm đến mặt phẳng .

Đáp án chuẩn:

Bài 10: Một công trường xây dựng nhà cao tầng đã thiết lập hệ tọa độ . Hãy kiểm tra tính song song hoặc vuông góc giữa các mặt kính , , (Hình 20) của một tòa nhà, biết:

;

; 

.

Đáp án chuẩn: