Công thức xác suất toàn phần và công thức Bayes

1. Công thức xác suất toàn phần

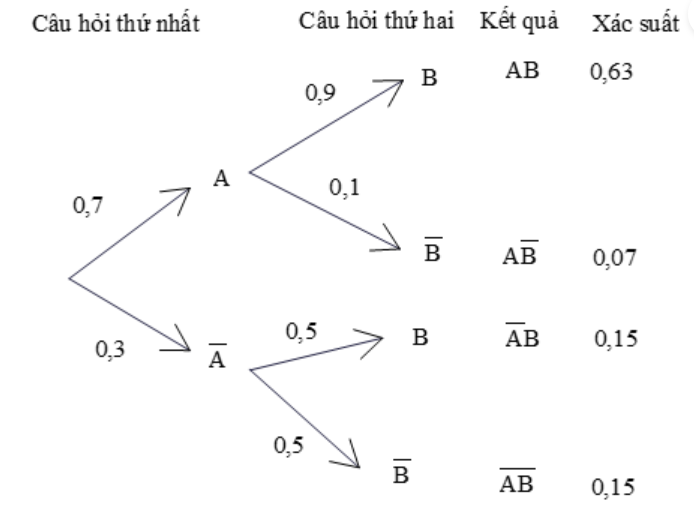
Khám phá 1: Chị An trả lời hai câu hỏi. Xác suất trả lời đúng câu hỏi thứ nhất là 0,7. Xác suất trả lời đúng câu hỏi thứ hai là 0,9 nếu chị An trả lời đúng câu hỏi thứ nhất và là 0,5 nếu chị An không trả lời đúng câu hỏi thứ nhất.

Gọi A là biến cố “Chị An trả lời đúng câu hỏi thứ nhất”

và B là biến cố “Chị An trả lời đúng câu hỏi thứ hai”. 

Hãy tìm các giá trị thích hợp điền vào các ô ? ở sơ đồ hình cây sau:

Đáp án chuẩn:

TH1: Vào mỗi buổi sáng ở tuyến phố H, xác suất xảy ra tắc đường khi trời mưa và không mưa lần lượt là 0,7 và 0,2. Xác suất có mưa vào một buổi sáng là 0,1. Tính xác suất để sáng đó tuyến phố H bị tắc đường.

Đáp án chuẩn:

2. Công thức Bayes

Khám phá 2: Khảo sát thị lực của 100 học sinh, ta thu được bảng số liệu sau:

Chọn ngẫu nhiên 1 bạn trong 100 học sinh trên.

a) Biết rằng bạn đó có tật khúc xạ, tính xác suất bạn đó là học sinh nam.

b) Biết rằng bạn đó là học sinh nam, tính xác suất bạn đó có tật khúc xạ.

Đáp án chuẩn:

a)

b)

TH2: Khi phát hiện một vật thể bay, xác suất một hệ thống radar phát cảnh báo là 0,9 nếu vật thể bay đó là mục tiêu thật và là 0,05 nếu đó là mục tiêu giả. Có 99% các vật thể bay là mục tiêu giả. Biết rằng hệ thống radar đang phát cảnh báo khi phát hiện một vật thể bay. Tính xác suất vật thể đó là mục tiêu thật.

Đáp án chuẩn:

15.38%.

Vận dụng: Người ta điều tra thấy ở một địa phương nọ có 2% tài xế sử dụng điện thoại di động khi lái xe. Trong các vụ tai nạn ở địa phương đó, người ta nhận thấy có 10% là do tài xế có sử dụng điện thoại khi lái xe gây ra. Hỏi việc sử dụng điện thoại di động khi lái xe làm tăng xác suất gây tai nạn lên bao nhiêu lần?

Đáp án chuẩn:

5 lần

BÀI TẬP

Bài tập 1: Hộp thứ nhất có 3 viên bi xanh và 6 viên bi đỏ. Hộp thứ hai có 3 viên bi xanh và 7 viên bi đỏ. Các viên bi có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên 1 viên bi từ hộp thứ nhất chuyển sang hộp thứ hai. Sau đó lại lấy ra ngẫu nhiên đồng thời 2 viên bi từ hộp thứ hai.

a) Tính xác suất để hai viên bi lấy ra từ hộp thứ hai là bi đỏ.

b) Biết rằng 2 viên bi lấy ra từ hộp thứ hai là bi đỏ, tính xác suất viên bi lấy ra từ hộp thứ nhất cũng là bi đỏ.

Đáp án chuẩn:

a) P =  

b) P =

Bài tập 2: Trong một trường học, tỉ lệ học sinh nữ là 52%. Tỉ lệ học sinh nữ và tỉ lệ học sinh nam tham gia câu lạc bộ nghệ thuật lần lượt là 18% và 15%. Gặp ngẫu nhiên 1 học sinh của trường.

a) Tính xác suất học sinh đó có tham gia câu lạc bộ nghệ thuật.

b) Biết rằng học sinh có tham gia câu lạc bộ nghệ thuật. Tính xác suất học sinh đó là nam.

Đáp án chuẩn:

a)

b)

Bài tập 3: Tỉ lệ người dân đã tiêm vắc xin phòng bệnh A ở một địa phương là 65%. Trong số những người đã tiêm phòng, tỉ lệ mắc bệnh A là 5% còn trong số những người chưa tiêm, tỉ lệ mắc bệnh A là 17%. Gặp ngẫu nhiên một người ở địa phương đó.

a) Tính xác suất người đó mắc bệnh A.

b) Biết rằng người đó mắc bệnh A. Tính xác suất người đó không tiêm vắc xin phòng bệnh A.

Đáp án chuẩn:

a) P = 0.092 

 b)

Bài tập 4: Ở một khu rừng nọ có 7 chú lùn, trong đó có 4 chú luôn nói thật, 3 chú còn lại nói thật với xác suất 0,5. Bạn Tuyết gặp ngẫu nhiên một chú lùn. Gọi A là biến cố “Chú lùn đó luôn nói thật” và B là biến cố “Chú lùn đó tự nhận mình luôn nói thật”.

a) Tính xác suất của các biến cố A và B.

b) Biết rằng chú lùn mà bạn Tuyết gặp tự nhận mình là người luôn nói thật. Tính xác suất để chú lùn đó luôn nói thật.

Đáp án chuẩn:

a) ;

b)