5 phút giải Toán 12 tập 2 chân trời sáng tạo trang 32
5 phút giải Toán 12 tập 2 chân trời sáng tạo trang 32. Giúp học sinh nhanh chóng, mất ít thời gian để giải bài. Tiêu chi bài giải: nhanh, ngắn, súc tích, đủ ý. Nhằm tạo ra bài giải tốt nhất. 5 phút giải bài, bằng ngày dài học tập.
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
BÀI 1. PHƯƠNG TRÌNH MẶT PHẲNG
PHẦN I. HỆ THỐNG BÀI TẬP CUỐI SGK
Bài 1: Viết phương trình của mặt phẳng:
a) Đi qua điểm ![]() và nhận
và nhận ![]() làm vectơ pháp tuyến;
làm vectơ pháp tuyến;
b) Đi qua điểm ![]() và song song với giá của mỗi vectơ
và song song với giá của mỗi vectơ ![]() và
và ![]() ;
;
c) Đi qua ba điểm ![]() ,
, ![]() và
và ![]() .
.
Bài 2: a) Lập phương trình của các mặt phẳng toạ độ ![]() ,
, ![]() ,
, ![]() .
.
b) Lập phương trình của các mặt phẳng đi qua điểm ![]() và lần lượt song song với các mặt phẳng tọa độ trên.
và lần lượt song song với các mặt phẳng tọa độ trên.
Bài 3: Cho tứ diện ![]() có các đỉnh
có các đỉnh ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
a) Hãy viết phương trình của các mặt phẳng ![]() và
và ![]() .
.
b) Hãy viết phương trình mặt phẳng ![]() đi qua cạnh
đi qua cạnh ![]() và song song với cạnh
và song song với cạnh ![]() .
.
Bài 4: Viết phương trình mặt phẳng ![]() đi qua điểm
đi qua điểm ![]() và song song với mặt phẳng
và song song với mặt phẳng ![]() .
.
Bài 5: Viết phương trình mặt phẳng ![]() đi qua hai điểm
đi qua hai điểm ![]() ,
, ![]() và vuông góc với mặt phẳng
và vuông góc với mặt phẳng ![]() .
.
Bài 6: Viết phương trình mặt phẳng ![]() đi qua điểm
đi qua điểm ![]() và vuông góc với hai mặt phẳng
và vuông góc với hai mặt phẳng ![]() ,
, ![]() .
.
Bài 7: Tính khoảng cách từ gốc tọa độ và từ điểm ![]() đến mặt phẳng
đến mặt phẳng ![]()
Bài 8: Tính khoảng cách giữa hai mặt phẳng song song ![]() và
và ![]() .
.
Bài 9: Cho hình chóp ![]() có đáy
có đáy ![]() là hình chữ nhật với
là hình chữ nhật với ![]() ,
, ![]() ,
, ![]() và
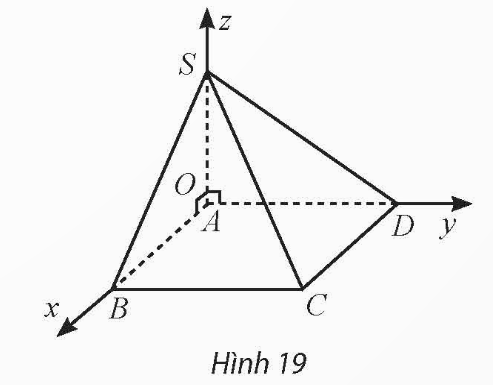
và ![]() . Bằng cách thiết lập hệ trục toạ độ
. Bằng cách thiết lập hệ trục toạ độ ![]() như Hình 19, tính khoảng cách từ điểm
như Hình 19, tính khoảng cách từ điểm ![]() đến mặt phẳng
đến mặt phẳng ![]() .
.
Bài 10: Một công trường xây dựng nhà cao tầng đã thiết lập hệ tọa độ ![]() . Hãy kiểm tra tính song song hoặc vuông góc giữa các mặt kính
. Hãy kiểm tra tính song song hoặc vuông góc giữa các mặt kính ![]() ,
, ![]() ,
, ![]() (Hình 20) của một tòa nhà, biết:
(Hình 20) của một tòa nhà, biết:
![]() ;
;
![]() ;
;
![]() .
.
PHẦN II. 5 PHÚT GIẢI BÀI TẬP CUỐI SGK
Bài 1: a) ![]()
b) ![]()
c) ![]()
Bài 2: a) Mặt phẳng ![]() có phương trình là:
có phương trình là: ![]()
Mặt phẳng ![]()
![]()
Mặt phẳng ![]()
![]()
b) Mặt phẳng ![]() song song với mặt phẳng
song song với mặt phẳng ![]() nên có dạng:
nên có dạng:
![]()
Mà ![]() thuộc
thuộc ![]() nên:
nên: ![]()
Mặt phẳng ![]() song song với mặt phẳng
song song với mặt phẳng ![]() nên có dạng:
nên có dạng:
![]()
Mà ![]() thuộc
thuộc ![]() nên:
nên: ![]()
Mặt phẳng ![]() song song với mặt phẳng
song song với mặt phẳng ![]() nên có dạng:
nên có dạng:
![]()
Mà ![]() thuộc
thuộc ![]() nên:
nên: ![]()
Bài 3: a)
Phương trình của ![]() là:
là:
![]()
Phương trình của ![]() là:
là:
![]()
b) Phương trình của ![]() là:
là:
![]()
Bài 4: ![]()
Bài 5: Phương trình của ![]() là:
là:
![]()
Bài 6: Phương trình của ![]() là:
là:
![]()
Bài 7: 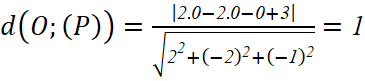
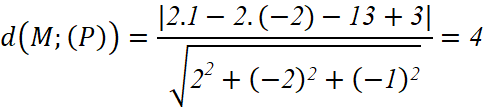
Bài 8: ![]()
Bài 9: ![]()
Bài 10: Các mặt phẳng ![]() có vecto pháp tuyến lần lượt là:
có vecto pháp tuyến lần lượt là: ![]() ,
, ![]() ,
, ![]()
![]() và
và ![]() . Vậy
. Vậy ![]()
![]() . Vậy
. Vậy ![]()
Mà ![]()
![]()
Nếu chưa hiểu - hãy xem: => Lời giải chi tiết ở đây
Nội dung quan tâm khác
Thêm kiến thức môn học
giải 5 phút Toán 12 tập 2 chân trời sáng tạo, giải Toán 12 tập 2 chân trời sáng tạo trang 32, giải Toán 12 tập 2 CTST trang 32
Giải bài tập những môn khác
Môn học lớp 12 KNTT
5 phút giải toán 12 KNTT
5 phút soạn bài văn 12 KNTT
Văn mẫu 12 KNTT
5 phút giải vật lí 12 KNTT
5 phút giải hoá học 12 KNTT
5 phút giải sinh học 12 KNTT
5 phút giải KTPL 12 KNTT
5 phút giải lịch sử 12 KNTT
5 phút giải địa lí 12 KNTT
5 phút giải CN lâm nghiệp 12 KNTT
5 phút giải CN điện - điện tử 12 KNTT
5 phút giải THUD12 KNTT
5 phút giải KHMT12 KNTT
5 phút giải HĐTN 12 KNTT
5 phút giải ANQP 12 KNTT
Môn học lớp 12 CTST
5 phút giải toán 12 CTST
5 phút soạn bài văn 12 CTST
Văn mẫu 12 CTST
5 phút giải vật lí 12 CTST
5 phút giải hoá học 12 CTST
5 phút giải sinh học 12 CTST
5 phút giải KTPL 12 CTST
5 phút giải lịch sử 12 CTST
5 phút giải địa lí 12 CTST
5 phút giải THUD 12 CTST
5 phút giải KHMT 12 CTST
5 phút giải HĐTN 12 bản 1 CTST
5 phút giải HĐTN 12 bản 2 CTST
Môn học lớp 12 cánh diều
5 phút giải toán 12 CD
5 phút soạn bài văn 12 CD
Văn mẫu 12 CD
5 phút giải vật lí 12 CD
5 phút giải hoá học 12 CD
5 phút giải sinh học 12 CD
5 phút giải KTPL 12 CD
5 phút giải lịch sử 12 CD
5 phút giải địa lí 12 CD
5 phút giải CN lâm nghiệp 12 CD
5 phút giải CN điện - điện tử 12 CD
5 phút giải THUD 12 CD
5 phút giải KHMT 12 CD
5 phút giải HĐTN 12 CD
5 phút giải ANQP 12 CD
Giải chuyên đề học tập lớp 12 kết nối tri thức
Giải chuyên đề Ngữ văn 12 Kết nối tri thức
Giải chuyên đề Toán 12 Kết nối tri thức
Giải chuyên đề Vật lí 12 Kết nối tri thức
Giải chuyên đề Hóa học 12 Kết nối tri thức
Giải chuyên đề Sinh học 12 Kết nối tri thức
Giải chuyên đề Kinh tế pháp luật 12 Kết nối tri thức
Giải chuyên đề Lịch sử 12 Kết nối tri thức
Giải chuyên đề Địa lí 12 Kết nối tri thức
Giải chuyên đề Tin học ứng dụng 12 Kết nối tri thức
Giải chuyên đề Khoa học máy tính 12 Kết nối tri thức
Giải chuyên đề Công nghệ 12 Điện - điện tử Kết nối tri thức
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Kết nối tri thức
Giải chuyên đề học tập lớp 12 chân trời sáng tạo
Giải chuyên đề Ngữ văn 12 Chân trời sáng tạo
Giải chuyên đề Toán 12 Chân trời sáng tạo
Giải chuyên đề Vật lí 12 Chân trời sáng tạo
Giải chuyên đề Hóa học 12 Chân trời sáng tạo
Giải chuyên đề Sinh học 12 Chân trời sáng tạo
Giải chuyên đề Kinh tế pháp luật 12 Chân trời sáng tạo
Giải chuyên đề Lịch sử 12 Chân trời sáng tạo
Giải chuyên đề Địa lí 12 Chân trời sáng tạo
Giải chuyên đề Tin học ứng dụng 12 Chân trời sáng tạo
Giải chuyên đề Khoa học máy tính 12 Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Điện - điện tử Chân trời sáng tạo
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Chân trời sáng tạo
Giải chuyên đề học tập lớp 12 cánh diều
Giải chuyên đề Ngữ văn 12 Cánh diều
Giải chuyên đề Toán 12 Cánh diều
Giải chuyên đề Vật lí 12 Cánh diều
Giải chuyên đề Hóa học 12 Cánh diều
Giải chuyên đề Sinh học 12 Cánh diều
Giải chuyên đề Kinh tế pháp luật 12 Cánh diều
Giải chuyên đề Lịch sử 12 Cánh diều
Giải chuyên đề Địa lí 12 Cánh diều
Giải chuyên đề Tin học ứng dụng 12 Cánh diều
Giải chuyên đề Khoa học máy tính 12 Cánh diều
Giải chuyên đề Công nghệ 12 Điện - điện tử Cánh diều
Giải chuyên đề Công nghệ 12 Lâm nghiệp thủy sản Cánh diều

Bình luận