Slide bài giảng Toán 9 Kết nối chương 9 Luyện tập chung (2)

Tóm lược nội dung

LUYÊN TẬP CHUNG

Giải chi tiết bài 9.31 trang 91 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Cho tam giác ABC có các đường cao AD,BE,CF. Chứng minh rằng BCEF, CAFD, ABDE là những tứ giác nội tiếp.

Trả lời rút gọn:

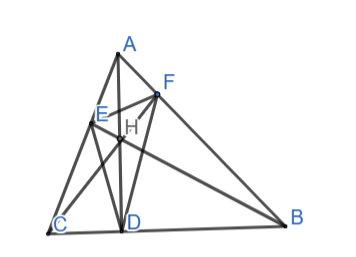
Xét tứ giác BCEF có ∠CEB = ∠CFB = 90ᵒ và cùng chắn cung BC.

=>BCEF nội tiếp đường tròn

Xét tứ giác CAFD có ∠AFC = ∠ADC = 90ᵒ và cùng chắn cung AC

=>CAFD nội tiếp đường tròn.

Xét tứ giác ABDE có ∠ADB = ∠AEB = 90ᵒ và cùng chắn cung AB

=>ABDE nội tiếp đường tròn.

Giải chi tiết bài 9.32 trang 91 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Cho tứ giác ABCD nội tiếp đường tròn (O), AB cắt CD tại E, AD cắt BC tại F như hình 9.58. Biết và , tính số đo các góc của tứ giác ABCD.

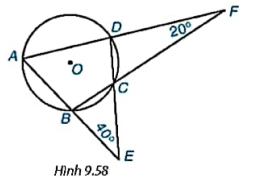
Trả lời rút gọn:

Ta có ADE + ∠ABF = 180ᵒ (Do ABCD nội tiếp đường tròn)

Lại có: ∠A + ∠E + ∠ADE = 180ᵒ và ∠A + ∠F + ∠ABF = 180ᵒ 

=>2. ∠A + 40 + 20 + ∠ADE + ∠ABF = 360

<=> 2∠A + ∠ADE + ∠ABF = 300

=> 2∠A + 180 = 300

<=> ∠A = 60ᵒ

Tứ giác ABCD nội tiếp =>∠DCB = 180 - ∠A = 120ᵒ

=> ∠DCF = 60ᵒ (hai góc ở vị trí kề bù)

Ta lại có ∠CDF = 180 - ∠DCF - ∠F (tổng 3 góc trong một tam giác)

=>∠CDF = 100ᵒ => ∠CDA = 80ᵒ (Hai góc kề bù)

Tứ giác ABCD nội tiếp =>∠CDA + ∠CBA = 180ᵒ

=> ∠CBA = 100ᵒ

Giải chi tiết bài 9.33 trang 91 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Cho hình vuông ABCD có cạnh bằng 4cm. Tính chu vi, diện tích của các đường tròn nội tiếp và ngoại tiếp hình vuông ABCD.

Trả lời rút gọn:

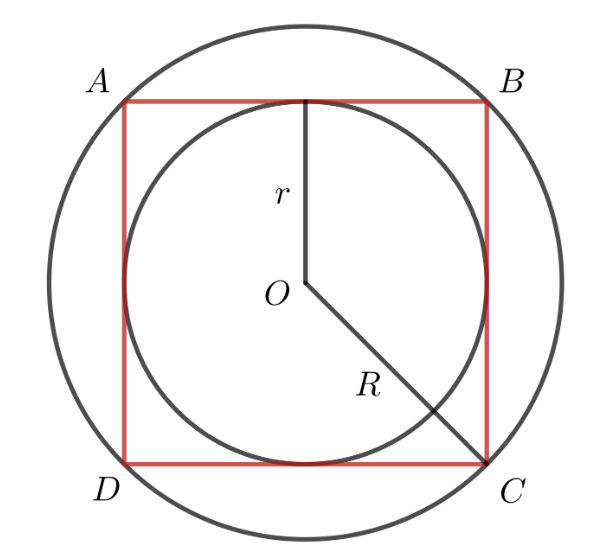
Gọi bán kính đường tròn nội tiếp hình vuông ABCD là: r

Gọi bán kính đường tròn ngoại tiếp hình vuông ABCD là: R

*Ta có r = 2 cm

Chu vi đường tròn nội tiếp hình vuông ABCD là 2r.3,14 = 12,56 cm

Diện tích đường tròn nội tiếp hình vuông ABCD là

* Ta có R = 2 cm

Chu vi đường tròn ngoại tiếp hình vuông ABCD là 2.R.3,14 = 17,76 cm

Diện tích đường tròn ngoại tiếp hình vuông ABCD là

Giải chi tiết bài 9.34 trang 91 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Biết rằng 4 đỉnh A,B,C,D của một hình vuông cùng nằm trên một đường tròn (O) theo thứ tự ngược chiều kim đồng hồ. Phép quay thuận chiều 45ᵒ biến các điểm A,B,C,D lần lượt thành các điểm E,F,G,H.

a) Vẽ đa giác EAFBGCHD.

b) Đa giác EAFBGCHD có phải là một bát giác đều không? Vì sao?

Trả lời rút gọn:

a)

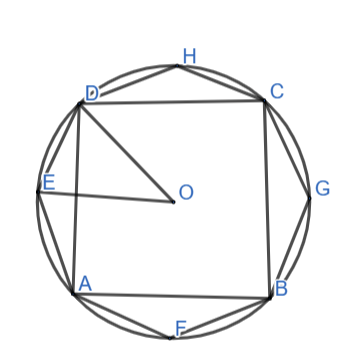
b) Số đo các cung nhỏ AB, BC, CD, DA bằng 90ᵒ (Do ABCD là hình vuông)

Phép quay thuận chiều 45ᵒ biến các điểm A,B,C,D lần lượt thành các điểm E,F,G,H

=>Số đo các cung nhỏ AF, FB, BG, GC, CH, HD, DE, EA đều bằng 45ᵒ

=> AF = FB = BG = GC = CH = HD = DE = EA

=> AFBGCHDE là hình bát giác đều.

Giải chi tiết bài 9.35 trang 91 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

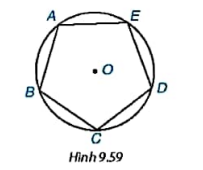
Cho ngũ giác đều ABCDE nội tiếp đường tròn (O) như hình 9.59.

a) Hãy tìm một phép quay thuận chiều tâm O biến điểm A thành điểm C.

b) Phép quay trên sẽ biến các điểm B,C,D,E lần lượt thành những điểm nào? Phép quay này có giữ nguyên ngũ giác đều ABCDE không?

Trả lời rút gọn:

a) Mỗi góc của ngũ giác đều là 108ᵒ

Ta có ∠BAE = 108 = sd cung lớn BE

=> góc lớn BOE = sd cung lớn BE = 216ᵒ

Mà ∠BOC + ∠COD + ∠DOE = 216ᵒ và ∠BOC = ∠COD = ∠DOE

=>∠BOC = ∠COD = ∠DOE = 72ᵒ

Phép quay thuận chiều tâm O biến điểm A thành điểm C là phép quay tâm O với góc quay 72.3 = 216ᵒ

b) - Phép quay trên sẽ biến các điểm B,C,D,E lần lượt thành những điểm: D, E, A, B

- Phép quay này có giữ nguyên ngũ giác đều ABCDE.

Giải chi tiết bài 9.36 trang 91 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

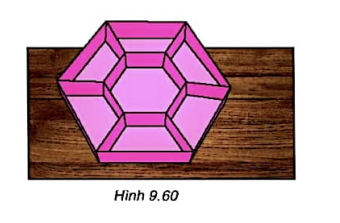
Người ta muốn làm một khay đựng bánh kẹo hình lục giác đều có cạnh 10 cm và chia thành 7 ngăn gồm một lục giác đều nhỏ và 6 hình thang cân như hình 9.60. Hỏi lục giác đều nhỏ phải có cạnh bằng bao nhiêu  để nó có diện tích bằng hai lần diện tích mỗi hình thang?

Trả lời rút gọn:

Gọi cạnh lục giác nhỏ là: a (cm)

Diện tích lục giác đều nhỏ =.tan() =

Gọi đường cao hạ từ đỉnh A của hình thang cân xuống đáy BC là h cm

Diện tích hình thang cân = (10 + a).

Theo đề bài, diện tích lục giác đều nhỏ gấp hai lần diện tích mỗi hình thang cân

=>

Diện tích khay = 6. (10 + a). +

Diện tích khay cũng bằng diện tích lục giác đều lớn 

=>     

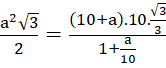
<=> 3=100+10a+

=>  a=5 cm

Vậy cạnh của lục giác đều nhỏ phải bằng 5cm để diện tich của nó bằng hai lần diện tích mỗi hình thang.