Slide bài giảng Toán 9 Kết nối bài 21: Giải bài toán bằng cách lập phương trình

Tóm lược nội dung

BÀI 21:GIẢI BÀI TOÁN BẰNG CÁCH LẬP PHƯƠNG TRÌNH

Mở đầu: Bác Lan gửi tiết kiệm 100 triệu đồng vào ngân hàng với kì hạn 12 tháng theo thể thức lãi kép. Sau năm thứ nhất, do chưa có nhu cầu sử dụng nên bác Lan không rút tiền ra mà tiếp tục gửi 12 tháng nữa, với lãi xuất như cũ. Sau hai năm bác Lan rút tiền ra thì nhận được 118,81 triệu đồng cả vốn lẫn lãi. Hỏi lãi suất gửi tiết kiệm là bao nhiêu?

Trả lời rút gọn:

Hoạt động 1 trang 25 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Gọi x là lãi suất gửi tiết kiệm của bác Lan(x được cho dưới dạng số thập phân).Hãy biều thị số tiền thu được(cả vốn lẫn lãi) của bác Lan sau kì gửi thứ nhất theo x.

Trả lời rút gọn:

Gọi x là lãi suất gửi tiết kiệm của bác Lan

Sau năm thứ nhất, số tiền bác Lan nhận được là: 

100 triệu + 100 triệu . x% = 100 triệu . (1 + x%).

Hoạt động 2 trang 25 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Hết kì gửi thứ nhất, bác Lan không rút tiền ra mà tiếp tục gửi tiết kiệm kì thứ hai với lãi suất như cũ. Hãy biểu thị số tiền thu được (cả vốn lẫn lãi) của bác Lan sau kì gửi thứ hai theo x.

Trả lời rút gọn:

Sau năm thứ nhất, bác Lan không rút tiền ra mà tiếp tục gửi thêm 12 tháng nữa. Do vậy, số tiền gốc để tính lãi cho năm thứ hai là 100 triệu * (1 + x%).

Sau 2 năm, bác Lan nhận được:

100 triệu . (1 + x%) + 100 triệu . (1 + x%) * x%

 = 100 triệu . (1 + x%) . (1 + x%)

Hoạt động 3 trang 25 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Dựa vào đề bài, viết phương trình ẩn x thu được và giải phương trình này để tìm x. Từ đó trả lời câu hỏi trong tình huống mở đầu.

Trả lời rút gọn:

Vì sau hai năm bác Lan nhận được 118,81 triệu đồng cả vốn lẫn lãi, nên ta có:

100 triệu . (1 + x%) . (1 + x%) = 118,81 triệu

=> (1 + x%)² = 1,1881

=> x% = 0,09

Vậy lãi suất gửi tiết kiệm là 9%/năm.

Luyện tập trang 27 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Một đội xe gồm các xe tải cùng loại, cần phải chở 120 tấn hàng. Tuy nhiên khi làm việc, có hai xe phải điều chuyển đi nơi khác nên mỗi xe phải chở thêm 3 tấn hàng. Hỏi đội xe đó có bao nhiêu chiếc xe tải?

Trả lời rút gọn:

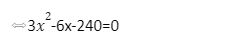
⬄x=10(tm) hoặc x=8(loại)

Vậy đội xe đó có 10 chiếc xe tải

GIẢI CHI TIẾT BÀI TẬP CUỐI SÁCH GIÁO KHOA 

Giải chi tiết bài 6.28 trang 27 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Một mảnh đất hình chữ nhật có diện tích 360 m2. Nếu tăng chiều rộng 3 m và giảm chiều dài 4 m thì diện tích mảnh đất không đổi. Tìm các kích thước của mảnh đất đó.

Trả lời rút gọn:

Giải chi tiết bài 6.29 trang 27 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Sau hai năm, số dân của một thành phố tăng từ 1 200 000 người lên 1 452 000 người. Hỏi trung bình mỗi năm dân số của thành phố đó tăng bao nhiêu phần trăm?

Trả lời rút gọn:

Số dân của thành phố tăng trong hai năm là:

1 452 000 - 1 200 000 = 252 000 người.

Tỉ lệ phần trăm dân số tăng trong hai năm là:

(252 000 / 1 200 000) .100% = 21%.

Tốc độ tăng trưởng trung bình mỗi năm là: 21% / 2 = 10,5%.

Giải chi tiết bài 6.30 trang 27 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Một thanh socola có dạng hình hộp chữ nhật với chiều dài 12cm chiều rộng 7cm và độ dày 3cm. Do giá nguyên liệu cacao tăng nhưng vẫn muốn giữ nguyên giá bán nên nhà sản xuất quyết định giảm 10% thể tích của mỗi thanh socola. Để thực hiện việc này, nhà sản xuất dự định làm thanh socola mới có cùng độ dày 3cm như thanh cũ, nhưng chiều dài và chiều rộng sẽ giảm đi  cùng một số cm. Hỏi kích thước của thanh socola mới là bao nhiêu?

Trả lời rút gọn:

Thể tích thanh socola cũ là: 12.7.3 = 252cm³

Thể tích thanh socola mới giảm 10% so với thanh cũ, nghĩa là thể tích thanh socola mới là 90% thể tích thanh socola cũ.

Thể tích thanh socola mới là: 252. 90% = 226,8cm³

Vì độ dày của thanh socola mới vẫn giữ nguyên 3cm, ta có thể tính chiều dài và chiều rộng mới theo công thức:

Chiều dài mới . Chiều rộng mới . Độ dày mới = Thể tích mới

=> Chiều dài mới . Chiều rộng mới = Thể tích mới / Độ dày mới=226,8cm³ / 3cm = 75,6cm²

Vì chiều dài và chiều rộng giảm đi cùng một số cm, ta gọi số cm giảm đi là x. Khi đó, ta có:

(12cm - x) . (7cm - x) = 75,6cm²

⬄x2-19x+8,4=0

⬄x=18,54(loại) hoặc x=0,45

Vậy kích thước của thanh socola mới là:

Chiều dài mới = 12cm - 0,45cm = 11,55cm

Chiều rộng mới = 7cm – 0,45cm = 6,55cm

Giải chi tiết bài 6.31 trang 27 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Một máy bay khởi hành từ Hà Nội vào Thành phố Hồ Chí Minh, sau đó nghỉ 96 phút và tiếp tục bay về Hà Nội với vận tốc lớn hơn vận tốc lúc đi là 100km/h. 

Tổng thời gian của cả hành trình, kể từ khi xuất phát từ Hà Nội đến khi quay về Hà Nội là 6 giờ. Tính vận tốc của máy bay lúc đi, biết quãng đường bay Hà Nội –Thành phố Hồ Chí Minh dài khoảng 1200km.

Trả lời rút gọn:

Tổng thời gian của cả hành trình là 6 giờ. Ta có phương trình:

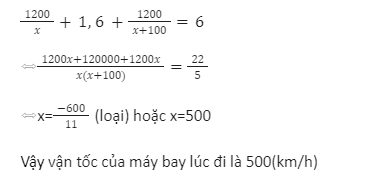
Giải chi tiết bài 6.32 trang 27 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Một ô tô khách khởi hành từ Hà Nội đi Hải Phòng. Sau đó 30 phút, một ô tô con xuất phát từ cùng địa điểm ở Hà Nội và cũng đi về Hải Phòng  trên cùng tuyến đường, với vận tốc lớn hơn của ô tô khách là 20km/h. Hai xe đến cùng một địa điểm ở Hải Phòng tại cùng một thời điểm.Hãy tính vận tốc của mỗi ô tô, biết rằng quãng đường Hà Nội-Hải Phòng khoảng 120km.

Trả lời rút gọn:

Đổi 30 phút=0,5 giờ

Gọi vận tốc của ô tô khách là x (km/h) x>0

Khi đó, vận tốc ô tô con là x+20 (km/h)

Giải chi tiết bài 6.33 trang 27 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Một xưởng may phải may 1500 chiếc áo trong thời gian quy định. Để hoàn thành sớm kế hoạch, mỗi ngày xưởng đã may được nhiều hơn 10 chiếc áo so với số áo phải may trong một ngáy theo kế hoạch. Do đó, ba ngày trước khi hết thời hạn, xưởng đã may được 1320 áo. Hỏi theo kế hoạch,mỗi ngày xưởng đó phải may xong bao nhiêu chiếc áo?

Trả lời rút gọn:

Gọi số áo mà xưởng đó phải may trong một ngày theo kế hoạc là x áo x>0