Slide bài giảng Toán 9 Kết nối bài 12: Một số hệ thức giữa cạnh, góc trong tam giác vuông và ứng dụng

Tóm lược nội dung

^{BÀI 12. MỘT SỐ HỆ THỨC GIỮA CẠNH, GÓC TRONG TAM GIÁC VUÔNG VÀ ỨNG DỤNG}

MỞ ĐẦU

Để đo chiều cao của một toà lâu đài (H.4.11), người ta đặt giác kế thẳng đứng tại điểm M. Quay ống ngắm của giác kế sao cho nhìn thấy đỉnh P’ của toà lâu đài dưới góc nhọn α. Sau đó, đặt giác kể thẳng đứng tại điểm N, NM = 20 m, thì nhìn thấy đỉnh P’ dưới góc nhọn β (β < α). Biết chiều cao giác kế là 1,6 m, jayx tính chiều cao của toà lâu đài.

Trả lời rút gọn:

-Xét ∆M’P’H vuông tại H ta có: M’H = P’H.cotα.

-Xét ∆N’P’H vuông tại H ta có: N’H = P’H.cotβ.

-Mà N’H = N’M’ + M’H = MN + M’H

=> P’H.cotβ = MN + P’H.cotα.

=>P’H.(cotβ – cotα) = MN =>

=> P’P = P’H + HP = (m).

1. HỆ THỨC GIỮA CẠNH HUYỀN VÀ CẠNH GÓC VUÔNG

Hoạt động 1 trang 74 sgk toán 9 tập 1 kết nối tri thức với cuộc sống

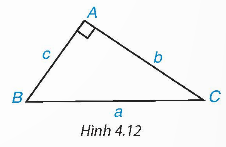
Cho tam giác ABC vuông tại A, cạnh huyền a và các cạnh góc vuông b, c (H.4.12).

a) Viết các tỉ số lượng giác sin, côsin của góc B và góc C theo độ dài các cạnh của tam giác ABC.

b) Tính mỗi cạnh góc vuông b và c theo cạnh huyền a và các tỉ số lượng giác trên của góc B và góc C.

Trả lời rút gọn:

a) 

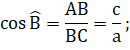
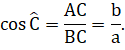
b) Ta có: 

Luyện tập 1 trang 75 sgk toán 9 tập 1 kết nối tri thức với cuộc sống

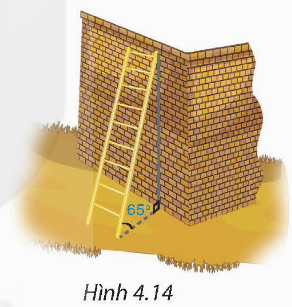
1. Một chiếc thang dài 3 m. Cần đặt chân thang cách chân tường một khoảng bằng bao nhiêu mét (làm tròn đến chữ số thập phân thứ hai) để nó tạo được với mặt đất một góc “an toàn” 65^o (tức là đảm bảo thang chắc chắn khi sử dụng) (H.4.14)?

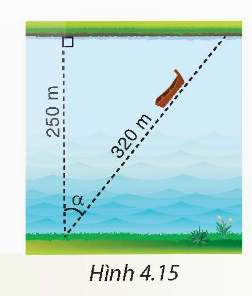
2. Một khúc sông rộng khoảng 250 m. Một con đò chèo qua sông bị dòng nước đẩy xiên nên phải chèo khoảng 320 m mới sang được bờ bên kia. Hỏi dòng nước đã đẩy con đò đi lệch một góc α bằng bao nhiêu độ (làm tròn đến phút)? (H.4.15).

Trả lời rút gọn:

1. Giả sử BC là độ dài thang và AB là khoảng cách từ chân thang đến chân tường. 

Ta có:AB = BC.cosB = 3.cos65° ≈ 1,27 (m).

Vậy cần đặt chân thang cách chân tường một khoảng 1,27 m để bó tạo được với mặt đất một góc “an toàn” 65°.

2. Giả sử AC là độ rộng của khúc sôg và BC là quãng đường con đò đã di chuyển từ bờ bên này sang bờ bên kia 

Dòng nước đã đẩy chiếc đò lệch đi một góc là:

- Vậy dòng nước đã đẩy con đò đi lệch một góc α ≈ 38°37’.

2. HỆ THỨC GIỮA HAI CẠNH GÓC VUÔNG

Hoạt động 2 trang 75 sgk toán 9 kết nối tri thức và cuộc sống

Xét tam giác ABC trong Hình 4.16.

a) Viết các tỉ lệ lượng giác tang, côtang của góc B và góc C theo b, c.

b) Tính mỗi cạnh góc vuông b và c theo cạnh góc vuông kia và các tỉ số lượng giác trên của góc B và góc C.

Trả lời rút gọn:

a) 

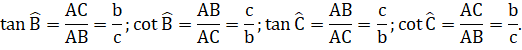
b) Ta có: 

Luyện tập 2 trang 76 sgk toán 9 tập 1 kết nối tri thức với cuộc sống

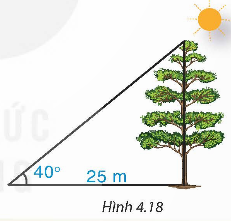
Bóng trên mặt đất của một cây dài 25 m. Tính chiều cao của cây (làm tròn đến dm), biết rằng tia nắng mặt trời tạo với mặt đất góc 40^o (H.4.18).

Trả lời rút gọn:

Theo Định lí 2, ta có chiều cao của tháp là: 

h = 25.tan40° ≈ 20,9775 (m) ≈ 210 (dm).

3. GIẢI TAM GIÁC VUÔNG

Luyện tập 3 trang 77 sgk toán 9 tập 1 kết nối tri thức với cuộc sống

Cho tam giác ABC vuông tại A có AB = 3, cạnh huyền BC = 8. Tính cạnh AC (làm tròn đến chữ số thập phân thứ ba) và các góc B, C (làm tròn đến độ).

Trả lời rút gọn:

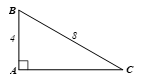
Ta có: AC² = BC² – AB² = 48 => AC = 6,928.

-Ta có .

=> .

Câu hỏi trang 77 sgk toán 9 tập 1 kết nối tri thức với cuộc sống

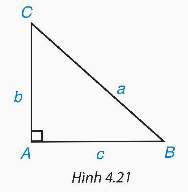
1. Hãy nêu cách giải tam giác ABC vuông tại A khi biết hai cạnh AB = c, AC = b hoặc AB = c, BC = a và không sử dụng định lí Pythagore (H.4.21).

2. Hãy nêu cách giải tam giác ABC vuông tại A khi biết cạnh góc vuông AB (hoặc cạnh huyền BC) và góc B.

Trả lời rút gọn:

1.  

- TH biết AB = c; AC =b

Ta có: 

Ta tính được góc B, và tính được góc C thông qua định lý tổng ba góc trong một tam giác. 

Sau khi tính được góc B, ta dùng tỉ số lượng giác =>

- TH AB = c, BC = a

Ta có:

Ta tính được góc B, và tính được góc C thông qua định lý tổng ba góc trong một tam giác. 

Sau khi tính được góc B, ta dùng tỉ số lượng giác => AC = c.tan B

2. 

* TH: biết cạnh góc vuông AB và góc B

-Xét tam giác ABC vuông tại A khi biết cạnh góc vuông AB (hoặc cạnh huyền BC) và góc B.

-Biết góc B ta tính được góc C thông qua định lý tổng ba góc trong một tam giác. -Tính cạnh BC ta dùng tỉ số lượng giác => và => AC = c.tan B 

* TH: cạnh huyền BC và góc B

-Biết góc B ta tính được góc C thông qua định lý tổng ba góc trong một tam giác. –Tính cạnh AB ta dùng  => AB = a. cos B và tỉ số lượng giác

Luyện tập 4 trang 77 sgk toán 9 tập 1 kết nối tri thức

Giải tam giác ABC vuông tại A, biết BC = 9,

Trả lời rút gọn:

sin C = => AB = 9.sin 53^o = 7,19.

cos C = => AC = 9.cos 53^o = 5,42.

Vận dụng trang 77 sgk toán 9 tập 1 kết nối tri thức với cuộc sống

Giải bài toán ở tình huống mở đầu với α = 27^o và β = 19^o.

Trả lời rút gọn:

-Xét ∆M’P’H vuông tại H, ta có: M’H = P’H.cotα.

-Xét ∆N’P’H vuông tại H ta có: N’H = P’H.cotβ.

-Mà N’H = N’M’ + M’H = MN + M’H

-Vì vậy P’H.cotβ = MN + P’H.cotα.

=> P’H.(cotβ – cotα) = MN nên

=> P’P = P’H + HP = 22,84 m.

Vậy chiều cao của tòa nhà là khoảng 22,84 (m).

4. GIẢI CHI TIẾT BÀI TẬP CUỐI SGK

Bài  4.8 trang 78 sgk toán 9 tập 1 kết nối tri thức với cuộc sống

Giải tam giác ABC vuông tại A có BC = a, AC = b, AB = c, trong các trường hợp:

a) a = 21, b = 18;             b) b = 10, ;                   c) c = 5, b = 3.

Trả lời rút gọn:

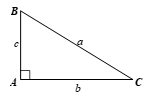
a) 

Theo định lí Pythagore ta có:  

Ta có: sin C =

b) 

cos C =

sin C =

c) -Theo định lí Pythagore:  

Ta có: sin C =

Bài  4.9 sgk trang 78 toán 9 tập 1 kết nối tri thức và cuộc sống

Tính góc nghiêng α của thùng xe chở rác trong Hình 4.22.

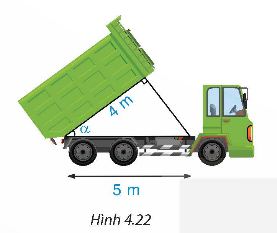
Trả lời rút gọn:

cos α  

Bài  4.10 trang 78 sgk toán 9 tập 1 kết nối tri thức và cuộc sống

Tìm góc nghiêng α và chiều rộng AB của mái nhà kho trong Hình 4.23.

Trả lời rút gọn:

tan α = => α = 3,43^o 

AB = =

Bài  4.11 trang 78 sgk toán 9 tập 1 kết nối tri thức và cuộc sống

Tính các góc của hình thoi có hai đường chéo dài và 2. 

Trả lời rút gọn:

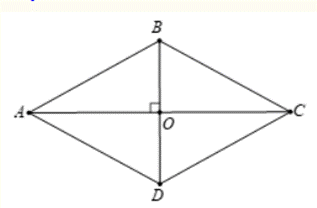
Ta có: AC =; BD = 2 và O là trung điểm BD và AC 

=> BO =1; AO = .

-Ta có:

-Vì AC là phân giác của góc BAD nên

=>

Bài  4.12 trang 78 sgk toán 9 tập 1 kết nối tri thức và cuộc sống

Cho hình thang ABCD (AD//BC) có AD = 16 cm, BC = 4 cm và

a) Kẻ đường cao CE của tam giác ACD. Chứng minh Rính sin của các góc và suy ra AC² = AE . AD. Từ đó tính AC.

b) Tính góc D của hình thang.

Trả lời rút gọn:

a) -Ta có:
nên

Ta có:

=>

-Hình thang ABCD có AD//BC và AB BC (do ) nên AB AD.

Tứ giác ABCE có => ABCE là hình chữ nhật.

=> AE = BC = 4 cm 

=> AC² = 4.16 = 64 nên AC = 8 cm

sin D = .

Bài  4.13 trang 78 sgk toán 9 tập 1 kết nối tri thức và cuộc sống

Một người đứng tại điểm A, cách gương phẳng đặt nằm trên mặt đất tại điểm B là 1,2 m, nhìn thấy hình ảnh phản chiếu qua gương B của ngọn cây (cây có gốc ở tại điểm C cách B là 4,8 m, B nằm giữa A và C). Biết khoảng cách từ mặt đất đến mắt người đó là 1,65 m. Tính chiều cao của cây (H.4.24).

Trả lời rút gọn:

CE = BC.tan

-Vậy chiều cao của cây là 6,6 m.