Slide bài giảng Toán 9 Kết nối bài 29: Tứ giác nội tiếp

Tóm lược nội dung

BÀI 29: TỨ GIÁC NỘI TIẾP

1. ĐƯỜNG TRÒN NGOẠI TIẾP MỘT TỨ GIÁC

Hoạt động 1 trang 80 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Cho tứ giác ABCD có Hãy giải thích vì sao bốn đỉnh của tứ giác ABCD cùng nằm trên một đường tròn có tâm là trung điểm O của đoạn thẳng BD.

Trả lời rút gọn:

ΔABD vuông tại A => Tâm đường tròn ngoại tiếp ΔABD nằm ở trung điểm của cạnh BD  (1)

ΔBCD vuông tại C=>Tâm đường tròn ngoại tiếp ΔBCD nằm ở trung điểm của cạnh BD (2)

Từ (1) và (2) =>OB = OD = OA = OC

=> A, B, C, D cùng thuộc đường tròn (O).

Hoạt động 2 trang 80 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Trên đường tròn (O), lấy các điểm A,B,C,D sao cho ABCD là tứ giác lồi (H9.29).Các đường trung trực của các cạnh AB,BC,CD,DA có đồng quy hay không?

Trả lời rút gọn:

ΔADC nội tiếp đường tròn tâm O =>Đường trung trực của AD, CD cắt nhau tại điểm O (1)

Tương tự: Đường trung trực của AB, BC cắt nhau tại điểm O. (2)

Từ 1 và 2=> Các đường trung trực của các cạnh AB, BC, CD, DA đồng quy tại O.

Hoạt động 3 trang 81 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Em hãy đo các góc đối nhau A và C của tứ giác ABCD trong HD2 và tính tổng  So sánh kết quả của em với các bạn.

Trả lời rút gọn:

=180^o

Kết quả giống của các bạn.

Luyện tập 1  trang 81 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Cho tam giác ABC có các đường cao BE,CF. Biết rằng

a) Chứng tỏ rằng tứ giác BCEF nội tiếp một đường tròn có tâm là trung điểm của cạnh BC.

b) Tính số đo của các góc BFE và CFE.

Trả lời rút gọn:

a)

Ta có: ∠BEC = ∠BFC = 90^o 

=> Tứ giác BCEF nội tiếp đường tròn có tâm là trung điểm của BC.

b) Từ câu a, ta có: ∠BFE + ∠BCE = 180^o(tổng hai góc đối trong tứ giác nội tiếp)

=> ∠BFE = 180 - 80 = 100 ^o

Có ∠CEF + ∠CBF = 180^o (tổng hai góc đối trong tứ giác nội tiếp)

=>∠CEF = 180 - 60 = 120^o

Thử thách nhỏ 1 trang 82 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Cho tứ giác ABCD, biết rằng các đường trung trực của ba đoạn thẳng AB,AC,AD đồng quy tại một điểm. Hãy giải thích vì sao ABCD là tứ giác nội tiếp.

Trả lời rút gọn:

ΔADC có ba đường trung trực tương ứng với ba cạnh cắt nhau tại O

=> OA = OD = OC (1)

ΔABC có 2 đường trung trực tương ứng với hai cạnh cắt nhau tại O

=> OA = OB = OC (2)

Từ 1 và 2 =>OA = OB = OC = OD

Vậy tứ giác ABCD nội tiếp đường tròn.

2. ĐƯỜNG TRÒN NGOẠI TIẾP HÌNH CHỮ NHẬT VÀ HÌNH VUÔNG

Hoạt động 4 trang 82 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Vẽ hình chữ nhật ABCD và giao điểm M của hai đường chéo AC và BD(H9.33).

a) Hãy giải thích vì sao điểm M cách đều bốn đỉnh của hình chữ nhật ABCD.

b) Chứng tỏ rằng hình chữ nhật ABCD nội tiếp một đường tròn có bán kính bằng nửa đường chéo hình chữ nhật.

Trả lời rút gọn:

a) M là giao điểm của AC và BD

=>MA = MB = MC = MD

=>M cách đều 4 đỉnh của hình chữ nhật ABCD

b) Từ câu a => Hình chữ nhật ABCD nội tiếp đường tròn tâm M và có bán kính bằng một nửa AC, BD hay bằng một nửa đường chéo của hình chữ nhật.

Hoạt động 5 trang 82 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Cho hình vuông ABCD có cạnh bằng 3cm(H9.34). Hãy xác định tâm, vẽ đường tròn ngoại tiếp hình vuông ABCD và cho biết bán kính của đường tròn đó.

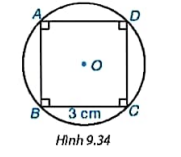
Trả lời rút gọn:

Tâm của đường tròn ngoại tiếp hình vuông ABCD chính là giao điểm của hai đường chéo AC và BD

Ta có: AC² = AB² + BC² =18

=> AC = BD = cm

Vậy bán kính của đường tròn ngoại tiếp hình vuông ABCD là  cm

Luyện tập 2  trang 83 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Cho hình thoi ABCD có các cạnh bằng 3cm. Gọi M,N,P,Q lần lượt là trung điểm của AB,BC,CA,AD. Chứng tỏ rằng tứ giác MNPQ là hình chữ nhật và tìm bán kính đường tròn ngoại tiếp của tứ giác đó.

Trả lời rút gọn:

Tac có: QM là đường trung bình của ΔABD (AQ = QD; AM = MB)

=> QM//BD và QM =   (1)

PN là đường trung bình của ΔCBD (CP = PD; CN = NB)

=>PN//BD và PN =    (2)

Từ 1 và 2 => MNPQ là hình bình hành (3)

Gọi giao điểm của AC và BD là O

Ta có AO ⊥ BD  =>AO ⊥ QM

Tương tự DO ⊥ AC

=> ∠MQB = 90^o (4)

Từ 3 và 4 =>MNPQ là hình chữ nhật.

=> Tâm đường tròn nội tiếp hình chữ nhật MNPQ là giao điểm của hai đường chéo MP,NQ

*Ta có: OM là đường trung bình của tam giác ABC (AM = MB; AO = OC)

=>OM =

Tương tự OP =

=>PM = BC = 3cm

=>OM =

Vậy bán kính đường tròn nội tiếp hình chữ nhật là 1,5cm

Thử thách nhỏ 2 trang 83 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Nếu các hình chữ nhật có chung một đường chéo (ví dụ như hai hình chữ nhật ABCD và AECF trong hình 9.36) thì các đỉnh của chúng có cùng nằm trên một đường tròn không?

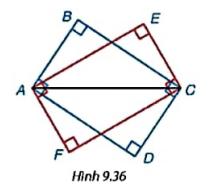
Trả lời rút gọn:

ΔABC vuông tại B => đường tròn ngoại tiếp ΔABC sẽ nằm ở trung điểm cạnh AC

Tương tự, đường tròn ngoại tiếp ΔAEC cũng nằm ở trung điểm của AC.

ΔADC vuông tại D => đường tròn ngoại tiếp ΔADC sẽ nằm ở trung điểm cạnh AC.

Tương tự, đường tròn ngoại tiếp ΔAFC cũng nằm ở trung điểm của AC.

Vậy các điểm A,B,E,C,D,F cùng thuộc một đường tròn.

3. GIẢI CHI TIẾT BÀI TẬP CUỐI SGK

Giải chi tiết bài 9.18 trang 83 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Cho ABCD là tứ giác nội tiếp. Tính số đo của các góc còn lại của tứ giác trong mỗi trường hợp sau:

Trả lời rút gọn:

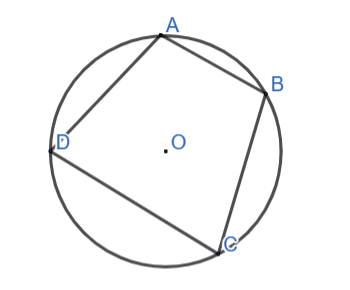
Theo tính chất tổng hai góc đối trong tứ giác nội tiếp ta có:

a) 

* ∠A + ∠C = 180^o => ∠C = 120^o

* ∠D + ∠B = 180^o => ∠D = 100^o

b) 

* ∠A + ∠C = 180^o => ∠A = 90^o

* ∠D + ∠B = 180^o => ∠D = 110^o

c) 

* ∠A + ∠C = 180^o => ∠A = 80^o

*∠D + ∠B = 180^o => ∠B = 120^o

d) 

* ∠A + ∠C = 180^o => ∠C = 100^o

* ∠D + ∠B = 180^o=> ∠B = 70^o

Giải chi tiết bài 9.19 trang 83 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Cho điểm I nằm ngoài đường tròn (O). Qua I kẻ hai đường thẳng lần lượt cắt (O) tại 4 điểm A,B và C,D sao cho A nằm giữa B và I, C nằm giữa D và I. Chứng minh rằng

Trả lời rút gọn:

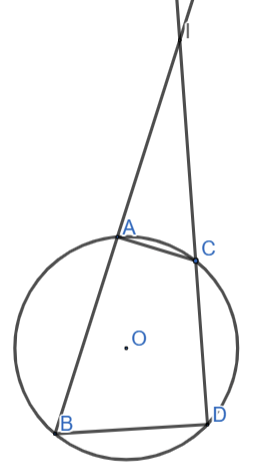
Ta có tứ giác ACDB nội tiếp đường tròn (O)

=> ∠BAC + ∠BDC = 180^o

Mà ∠BAC + ∠IAC = 180^o (hai góc ở vị trí kề bù)

=> ∠BDC = ∠IAC hay ∠IAC = ∠IDB(dpcm)

Lại có: ΔIAC ∼ ΔIDB (Góc I chung; ∠IAC = ∠IDB)

=>∠ICA = ∠IDB (dpcm)

Và => IA.IB = IC.ID(dpcm)

Giải chi tiết bài 9.20 trang 83 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Cho hình bình hành ABCD nội tiếp đường tròn (O). Chứng minh rằng ABCD là hình chữ nhật.

Trả lời rút gọn:

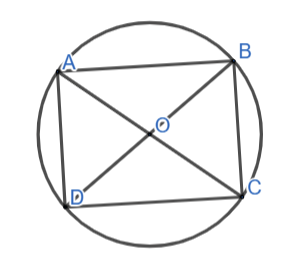
Ta có ABCD nội tiếp đường tròn (O)

=>∠BAD + ∠BCD = 180^o

Mà ∠ABD + ∠ADC = 180^o (hai góc ở vị trí trong cùng phía)

=>∠ADC = ∠DCB

Mà ∠ADC + ∠DCB = 180^o (hai góc ở vị trí trong cùng phía)

=>∠ADC = ∠DCB = 90 ^o

=>ABCD là hình chữ nhật

Giải chi tiết bài 9.21 trang 83 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Cho hình thang ABCD(AB//CD) nội tiếp đường tròn (O). Chứng minh rằng ABCD là hình thang cân.

Trả lời rút gọn:

Ta có hình thang ABCD nội tiếp đường tròn (O)

=>∠BAD + ∠BCD = 180^o

Mà ∠BAD + ∠ADC = 180^o(hai góc ở vị trí trong cùng phía)

=> ∠BCD = ∠ADC

=> Hình thang ABCD là hình thang cân 

Giải chi tiết bài 9.22 trang 83 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Tính diện tích của một hình chữ nhật, biết rằng hình chữ nhật đó có chiều dài gấp hai lần chiều rộng và bán kính đường tròn ngoại tiếp bằng 2,5cm

Trả lời rút gọn:

Gọi hình chữ nhật trong đề bài là ABCD và tâm đường tròn ngoại tiếp là O, với AB = 2BC

Bán kinh bằng 2,5cm =>AC = BD = 2.OA = 5 cm

Ta có

=>

=> 5

=> BC =

=> AB = 2BC = 2

Vậy chiều dài của hình chữ nhật là 2; chiều rộng là

Giải chi tiết bài 9.23 trang 83 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Người ta muốn dựng một khung cổng hình chữ nhật rộng 4m và cao 3m., bên ngoài khung cồng được bao bởi một khung thép dạng nửa đường tròn như hình 9.37. Tính chiều dài của đoạn thép làm khung cửa đường tròn đó.

Trả lời rút gọn:

Hình chữ nhật với chiều dài 6m ; chiều rộng 4m nội tiếp đường tròn. 

Ta xét nửa trên :

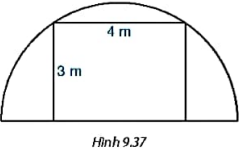
Chu vi của hình tròn là: d.3,14 = 8.3,14 = 25,12 m

Vậy chiều dài đoạn thép là 25,12m

Trả lời rút gọn:

a)                  

Ta có: ∠BEC = ∠BFC = 90^o 

=> Tứ giác BCEF nội tiếp đường tròn có tâm là trung điểm của BC.

b) Từ câu a, ta có: ∠BFE + ∠BCE = 180^o(tổng hai góc đối trong tứ giác nội tiếp)

=> ∠BFE = 180-80 = 100 ^o

Có ∠CEF + ∠CBF = 180^o (tổng hai góc đối trong tứ giác nội tiếp)

=>∠CEF = 180 - 60 = 120^o

Thử thách nhỏ 1 trang 82 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Cho tứ giác ABCD, biết rằng các đường trung trực của ba đoạn thẳng AB,AC,AD đồng quy tại một điểm. Hãy giải thích vì sao ABCD là tứ giác nội tiếp.

Trả lời rút gọn:

ΔADC có ba đường trung trực tương ứng với ba cạnh cắt nhau tại O

=> OA = OD = OC (1)

ΔABC có 2 đường trung trực tương ứng với hai cạnh cắt nhau tại O

=> OA = OB = OC (2)

Từ 1 và 2 =>OA = OB = OC = OD

Vậy tứ giác ABCD nội tiếp đường tròn.

2. ĐƯỜNG TRÒN NGOẠI TIẾP HÌNH CHỮ NHẬT VÀ HÌNH VUÔNG

Hoạt động 4 trang 82 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Vẽ hình chữ nhật ABCD và giao điểm M của hai đường chéo AC và BD(H9.33).

a) Hãy giải thích vì sao điểm M cách đều bốn đỉnh của hình chữ nhật ABCD.

b) Chứng tỏ rằng hình chữ nhật ABCD nội tiếp một đường tròn có bán kính bằng nửa đường chéo hình chữ nhật.

Trả lời rút gọn:

a) M là giao điểm của AC và BD

=>MA = MB = MC = MD

=>M cách đều 4 đỉnh của hình chữ nhật ABCD

b) Từ câu a => Hình chữ nhật ABCD nội tiếp đường tròn tâm M và có bán kính bằng một nửa AC, BD hay bằng một nửa đường chéo của hình chữ nhật.

Hoạt động 5 trang 82 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Cho hình vuông ABCD có cạnh bằng 3cm(H9.34). Hãy xác định tâm, vẽ đường tròn ngoại tiếp hình vuông ABCD và cho biết bán kính của đường tròn đó.

Trả lời rút gọn:

Tâm của đường tròn ngoại tiếp hình vuông ABCD chính là giao điểm của hai đường chéo AC và BD

Ta có: AC² = AB² + BC² =18

=> AC = BD = cm

Vậy bán kính của đường tròn ngoại tiếp hình vuông ABCD là  cm

Luyện tập 2  trang 83 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Cho hình thoi ABCD có các cạnh bằng 3cm. Gọi M,N,P,Q lần lượt là trung điểm của AB,BC,CA,AD. Chứng tỏ rằng tứ giác MNPQ là hình chữ nhật và tìm bán kính đường tròn ngoại tiếp của tứ giác đó.

Trả lời rút gọn:

Tac có: QM là đường trung bình của ΔABD (AQ = QD; AM = MB)

=> QM//BD và QM =   (1)

PN là đường trung bình của ΔCBD (CP = PD; CN = NB)

=>PN//BD và PN =    (2)

Từ 1 và 2 => MNPQ là hình bình hành (3)

Gọi giao điểm của AC và BD là O

Ta có AO ⊥ BD  =>AO ⊥ QM

Tương tự DO ⊥ AC

=> ∠MQB = 90^o (4)

Từ 3 và 4 =>MNPQ là hình chữ nhật.

=> Tâm đường tròn nội tiếp hình chữ nhật MNPQ là giao điểm của hai đường chéo MP,NQ

*Ta có: OM là đường trung bình của tam giác ABC (AM = MB; AO = OC)

=>OM =

Tương tự OP =

=>PM = BC = 3cm

=>OM =

Vậy bán kính đường tròn nội tiếp hình chữ nhật là 1,5cm

Thử thách nhỏ 2 trang 83 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Nếu các hình chữ nhật có chung một đường chéo (ví dụ như hai hình chữ nhật ABCD và AECF trong hình 9.36) thì các đỉnh của chúng có cùng nằm trên một đường tròn không?

Trả lời rút gọn:

ΔABC vuông tại B => đường tròn ngoại tiếp ΔABC sẽ nằm ở trung điểm cạnh AC

Tương tự, đường tròn ngoại tiếp ΔAEC cũng nằm ở trung điểm của AC.

ΔADC vuông tại D => đường tròn ngoại tiếp ΔADC sẽ nằm ở trung điểm cạnh AC.

Tương tự, đường tròn ngoại tiếp ΔAFC cũng nằm ở trung điểm của AC.

Vậy các điểm A,B,E,C,D,F cùng thuộc một đường tròn.

3. GIẢI CHI TIẾT BÀI TẬP CUỐI SGK

Giải chi tiết bài 9.18 trang 83 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Cho ABCD là tứ giác nội tiếp. Tính số đo của các góc còn lại của tứ giác trong mỗi trường hợp sau:

Trả lời rút gọn:

Theo tính chất tổng hai góc đối trong tứ giác nội tiếp ta có:

a) 

* ∠A + ∠C = 180^o => ∠C = 120^o

* ∠D + ∠B = 180^o => ∠D = 100^o

b) 

* ∠A + ∠C = 180^o => ∠A = 90^o

* ∠D+ ∠B = 180^o => ∠D = 110^o

c) 

* ∠A+ ∠C = 180^o => ∠A = 80^o

*∠D+ ∠B = 180^o => ∠B = 120^o

d) 

* ∠A + ∠C = 180^o => ∠C = 100^o

* ∠D + ∠B = 180^o=> ∠B = 70^o

Giải chi tiết bài 9.19 trang 83 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Cho điểm I nằm ngoài đường tròn (O). Qua I kẻ hai đường thẳng lần lượt cắt (O) tại 4 điểm A,B và C,D sao cho A nằm giữa B và I, C nằm giữa D và I. Chứng minh rằng

Trả lời rút gọn:

Ta có tứ giác ACDB nội tiếp đường tròn (O)

=> ∠BAC + ∠BDC = 180^o

Mà ∠BAC + ∠IAC = 180^o (hai góc ở vị trí kề bù)

=> ∠BDC = ∠IAC hay ∠IAC = ∠IDB(dpcm)

Lại có: ΔIAC ∼ ΔIDB (Góc I chung; ∠IAC = ∠IDB)

=>∠ICA = ∠IDB (dpcm)

Và => IA.IB = IC.ID(dpcm)

Giải chi tiết bài 9.20 trang 83 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Cho hình bình hành ABCD nội tiếp đường tròn (O). Chứng minh rằng ABCD là hình chữ nhật.

Trả lời rút gọn:

Ta có ABCD nội tiếp đường tròn (O)

=>∠BAD + ∠BCD = 180^o

Mà ∠ABD + ∠ADC = 180^o (hai góc ở vị trí trong cùng phía)

=>∠ADC = ∠DCB

Mà ∠ADC + ∠DCB = 180^o (hai góc ở vị trí trong cùng phía)

=>∠ADC = ∠DCB = 90 ^o

=>ABCD là hình chữ nhật

Giải chi tiết bài 9.21 trang 83 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Cho hình thang ABCD(AB//CD) nội tiếp đường tròn (O). Chứng minh rằng ABCD là hình thang cân.

Trả lời rút gọn:

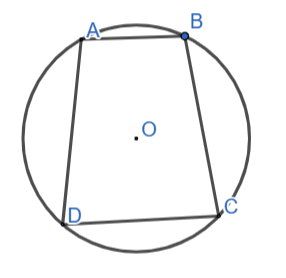
Ta có hình thang ABCD nội tiếp đường tròn (O)

=>∠BAD + ∠BCD = 180^o

Mà ∠BAD + ∠ADC = 180^o(hai góc ở vị trí trong cùng phía)

=> ∠BCD = ∠ADC

=> Hình thang ABCD là hình thang cân 

Giải chi tiết bài 9.22 trang 83 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Tính diện tích của một hình chữ nhật, biết rằng hình chữ nhật đó có chiều dài gấp hai lần chiều rộng và bán kính đường tròn ngoại tiếp bằng 2,5cm

Trả lời rút gọn:

Gọi hình chữ nhật trong đề bài là ABCD và tâm đường tròn ngoại tiếp là O, với AB=2BC

Bán kinh bằng 2,5cm =>AC = BD = 2.OA = 5 cm

Ta có

=>

=>5

=>BC =

=>AB = 2BC = 2

Vậy chiều dài của hình chữ nhật là 2; chiều rộng là

Giải chi tiết bài 9.23 trang 83 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Người ta muốn dựng một khung cổng hình chữ nhật rộng 4m và cao 3m., bên ngoài khung cồng được bao bởi một khung thép dạng nửa đường tròn như hình 9.37. Tính chiều dài của đoạn thép làm khung cửa đường tròn đó.

Trả lời rút gọn:

Hình chữ nhật với chiều dài 6m ; chiều rộng 4m nội tiếp đường tròn. 

Ta xét nửa trên :

Chu vi của hình tròn là: d.3,14=8.3,14=25,12 m

Vậy chiều dài đoạn thép là 25,12m