Slide bài giảng Toán 9 Kết nối bài 28: Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác

Tóm lược nội dung

BÀI 28: ĐƯỜNG TRÒN NGOẠI TIẾP VÀ ĐƯỜNG TRÒN NỘI TIẾP MỘT TAM GIÁC

Mở đầu: Cho trước một tam giác ABC. Bằng thước kẻ và compa, em có thể vẽ được một đường tròn đi qua ba đỉnh của tam giác và đường tròn tiếp xúc với cả ba cạnh của tam giác không?

Trả lời rút gọn:

*Vẽ đường tròn tiếp xúc với 3 cạnh của tam giác

Bước 1: Vẽ tam giác ABC

Bước 2: Kẻ 3 tia phân giác của mỗi góc A,B,C

Từ giao điểm của 3 đường phân giác,đặt đầu cố định compa vào vị trí đó. Đầu còn lại của compa mở rộng đến cạnh của tam giác, và xoay 1 vòng.

Ta được đường tròn tiếp xúc với cả ba cạnh của tam giác.

*Vẽ đường tròn đi qua 3 đỉnh của tam giác:

Kẻ 3 đường trung trực tương ứng với 3 cạnh của tam giác ABC.

Giao của 3 đường vừa kẻ chính là tâm của đường tròn đi qua 3 đỉnh của tam giác ABC.

1. ĐƯỜNG TRÒN NGOẠI TIẾP MỘT TAM GIÁC

Hoạt động 1 trang 72 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Cho d là đường trung trực của đoạn thẳng AB và O là một điểm trên d(H9.12). Hỏi đường tròn tâm O đi qua A thì có đi qua B không?

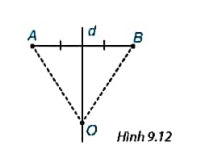
Trả lời rút gọn:

Ta có: OA = OB (tính chất đường trung trực)

=> Đường tròn tâm O đi qua A thì có đi qua B.

Hoạt động 2 trang 72 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Cho tam giác ABC có ba đường trung trực đồng quy tại O (H9.13). Hãy giải thích tại sao đường tròn (O;OA) đi qua ba đỉnh của tam giác ABC.

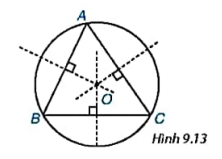
Trả lời rút gọn:

Ta có: OA = OB = OC (ba đường trung trực đồng quy tại O)

=> Đường tròn (O;OA) đi qua ba đỉnh của tam giác ABC.

Câu hỏi trang 73 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Hãy kể tên bốn tam giác nội tiếp đường tròn (O) trong hình 9.14

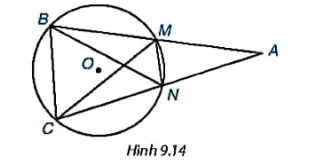
Trả lời rút gọn:

ΔBMC; ΔBNC; ΔMBN; ΔMCN

Hoạt động 3 trang 73 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

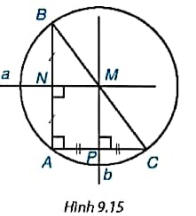
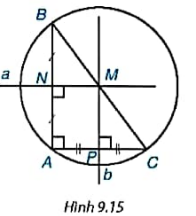
Cho tam giác ABC vuông tại đỉnh A(H9.15). Gọi N, P lần lượt là trung điểm của các cạnh AB và AC.

a) Vẽ hai đường trung trực a, b của các cạnh AB, AC cắt nhau tại M.

b) Hãy giải thích vì sao MN, MP là các đường trung bình của tam giác ABC.

c) Hãy giải thích vì sao M là trung điêm của BC, từ đó suy ra đường tròn ngoại tiếp của tam giác ABC có tâm M và bán kính MB = MC = .

Trả lời rút gọn:

a)

b) Ta có BN = NA; MN ⊥ AB (gt)

=> MN là đường trung bình của tam giác ABC

Lại có: AP = PC; MP⊥AC (gt)

=> MP là đường trung bình của tam giác ABC

c) Theo câu b, ta có: MB = MC = .

Vậy đường tròn ngoại tiếp của tam giác ABC có tâm M và bán kính MB = MC = .

Luyện tập 1 trang 73 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Cho tam giác ABC có AC = 3cm, AB = 4cm và BC = 5cm. Tính bán kính của đường tròn ngoại tiếp tam giác ABC

Trả lời rút gọn:

Ta có: ΔABC vuông tại A (Do = )

Lấy O là trung điểm BC và vẽ đường tròn (O) đi qua A. Khi đó, (O;OB) là đường tròn ngoại tiếp ΔABC.

=> OB = = 2,5cm                            

Vậy bán kính đường tròn ngoại tiếp ΔABC là 2,5cm

Hoạt động 4 trang 73 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

a) Vẽ tam giác đều ABC. Hãy trình bày các cách xác định tâm của đường tròn ngoại tiếp tam giác ABC và vẽ đường tròn đó.

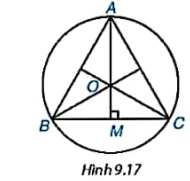
b) Giải thích vì sao tâm O của đường tròn ngoại tiếp tam giác ABC trùng với trọng tâm của tam giác đó (H9.17)

c) Giải thích vì sao (M là trung điểm của BC)

Trả lời rút gọn:

a)

Giao điểm của ba đường trung trực tương ứng với 3 cạnh của tam giác chính là tâm đường tròn ngoại tiếp tam giác.

b) Vì ΔABC là tam giác đều, nên trọng tâm trùng với trực tâm.

Nên tâm của đường tròn ngoại tiếp tam giác O trùng với trọng tâm của tam giác đó.

c)  Ta có: ∠ABC = sd cung nhỏ AC

Mà ΔABC là tam giác đều =>BO là tia phân giác của ∠ABC.

=>∠OBM = ∠ABC ^o (đpcm)

Lại có

=>AM =

AM =     

AM =

AM = MC.

AM = .BC

Mà AO = .AM (Do O là trọng tâm của ΔABC)

AO = OB =.BC (đpcm)

Luyện tập 2 trang 74 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

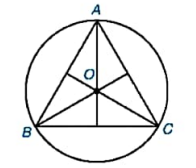
Cho tam giác đều ABC nội tiếp đường tròn (O) có bán kính 4cm. Tính độ dài các cạnh của tam giác.

Trả lời rút gọn:

OA = OB = OC = 4= .BC

=>BC = AB = AC = 4cm

2. ĐƯỜNG TRÒN NỘI TIẾP MỘT TAM GIÁC

Hoạt động 5 trang 74 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

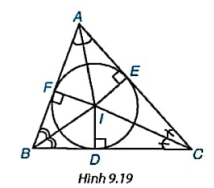
Cho tam giác ABC có ba đường phân giác đồng quy tại điểm I. Gọi D,E,F lần lượt là chân các đường vuông góc kẻ từ I xuống các cạnh BC,CA và AB(H9.19).

a) Hãy giải thích vì sao các điểm D, E, F cùng nằm trên một đường tròn có tâm I.

b) Gọi (I) là đường tròn trên. Hãy giải thích vì sao (I) tiếp xúc với các cạnh của tam giác ABC.

Trả lời rút gọn:

a)  Ta có: ΔCEI ∼  ΔCDI (∠ECI = ∠DCI; CI chung) =>ID = IE(1)

Tương tự: ΔAFI∼ ΔAEI (ch-gn) =>IF = IE(2)

Từ (1) và (2) => IE = IF = ID

=> Các điểm D, E, F cùng nằm trên một đường tròn có tâm I.

b) Vì D, E, F thuộc các cạnh của tam giác ABC

=> (I) tiếp xúc với các cạnh của tam giác ABC.

Câu hỏi trang 75 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Mỗi tam giác có bao nhiêu đường tròn nội tiếp? Có bao nhiêu tam giác cùng ngoại tiếp một đường tròn?

Trả lời rút gọn:

- Mỗi tam giác có duy nhất một đường tròn nội tiếp.

- Có vô số tam giác cùng ngoại tiếp một đường tròn.

Hoạt động 6 trang 75 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Cho tam giác ABC đều có trọng tâm G.

a) Giải thích vì sao G cũng là tâm đường tròn nội tiếp tam giác ABC.

b) Từ đó, giải thích vì sao bán kính đường tròn nội tiếp tam giác ABC bằng một nửa bán kính đường tròn ngoại tiếp tam giác ABC và bằng .BC.

Trả lời rút gọn:

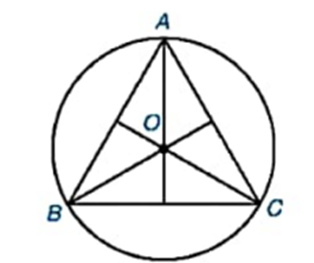
a)  Tam giác ABC đều => trực tâm sẽ trùng với giao điểm của ba đường phân giác => Đường tròn ngoại tiếp sẽ trùng với tâm đường tròn nội tiếp.

b) Gọi OC là bán kính đường tròn ngoại tiếp ΔABC.

OI là bán kính đường tròn nội tiếp ΔABC.

Có OC = OB = BC =>OB = BI

Có OI = BI => OI = OB

=> OI =BC

Vậy bán kính đường tròn ngoại tiếp ΔABC gấp đôi bán kính đường tròn nội tiếp tam giác ABC

Và bán kính đường tròn nội tiếp ΔABC là BC

Thực hành trang 75 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Vẽ đường tròn nội tiếp của tam giác ABC bằng thước kẻ và compa theo các bước sau:

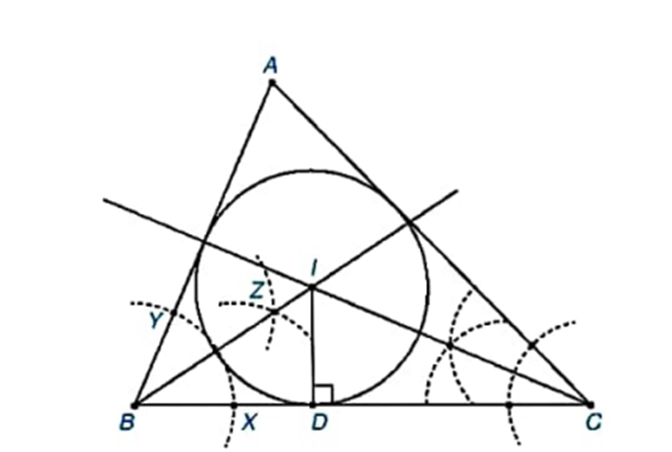
- Vẽ tia phân giác góc B như sau: Dùng compa vẽ một cung trong tâm B cắt hai cạnh BC, BA lần lượt tại X và Y. Vẽ hai cung tròn tâm X,Y có cùng bán kính, hai cung này cắt nhau tại một điểm Z khác B. Kẻ tia BZ ta được tia phân giác góc B.

- Tương tự,vẽ tia phân giác góc C , cắt tia BZ tại I.

- Vẽ đường cao ID từ I xuống BC(D thuộc BC). Vẽ đường tròn (I;ID)

Khi đó đường tròn (I;ID) là đường tròn nội tiếp tam giác ABC cần vẽ.

Trả lời rút gọn:

3. GIẢI CHI TIẾT BÀI TẬP CUỐI SGK

Giải chi tiết bài 9.7 trang 76 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Cho đường tròn (O) ngoại tiếp tam giác ABC. Tính bán kính của (O), biết rằng tam giác ABC vuông cân tại A và có cạnh bên bằng cm

Trả lời rút gọn:

Ta có: OA = OB = (Do tam giác ABC vuông cân tại A)

Bán kính của (O) bằng (cm)

Giải chi tiết bài 9.8 trang 76 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Cho tam giác đều ABC nội tiếp đường tròn (O). Biết rằng đường tròn (O) co bán kính bằng 3cm. Tính diện tích tam giác ABC.

Trả lời rút gọn:

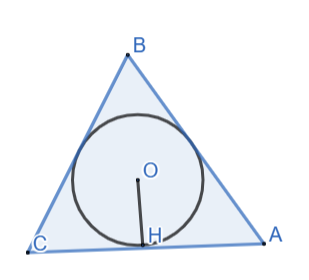
Gọi OH là bán kính đường tròn nội tiếp tam giác ABC.

ΔABC đều => OH =AB = 3cm

=> AB = 6cm

= 27

Giải chi tiết bài 9.9 trang 76 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Cho tam giác ABC nội tiếp đường tròn (O).Gọi H là trực tâm của tam giác ABC. Chứng minh rằng

Trả lời rút gọn:

Giải chi tiết bài 9.10 trang 76 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Cho đường tròn (I) nội tiếp tam giác ABC với các tiếp điểm trên cạnh AB,AC lần lượt là E,F. Chứng minh rằng  

Trả lời rút gọn:

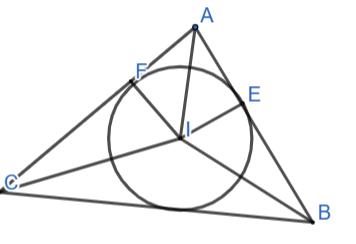
Giải chi tiết bài 9.11 trang 76 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Cho tam giác đều ABC ngoại tiếp đường tròn (I). Tính độ dài các cạnh của tam giác ABC biết rằng bán kính của (I) bằng 1cm.

Trả lời rút gọn:

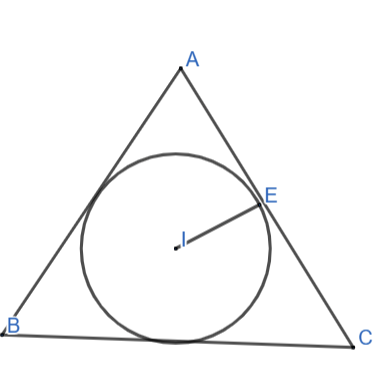
Gọi IE là bán kính đường tròn nội tiếp tam giác ABC.

Tam giác ABC đều=> tâm đường tròn nội tiếp tam giác trùng với tâm đường tròn ngoại tiếp tam giác.

=> IE = AB = 1cm =>AB = 2 cm

Vậy AB = BC = CA = 2 cm

Giải chi tiết bài 9.12 trang 76 sgk toán 9 tập 2 kết nối tri thức với cuộc sống

Người ta muốn làm một khung gỗ hình tam giác đều để đặt vừa khít một chiếc đồng hồ hình tròn có đường kính 30cm(H9.23). Hỏi độ dài các cạnh(phía bên trong) của khung gỗ phải bằng bao nhiêu?

Trả lời rút gọn:

Khung gỗ là hình tam giác đều => Tâm của đường tròn ngoại tiếp khung gỗ trùng với tâm của đường tròn nội tiếp khung gỗ.

=> Bán kính của đồng hồ =.Cạnh của khung gỗ.

=> Cạnh của khung gỗ là 30cm