Giải khám phá 4 trang 43 chuyên đề toán 10 chân trời sáng tạo
4. ĐƯỜNG CHUẨN
Hoạt động khám phá 4: Cho điểm M(x; y) trên elip (E):
$\frac{x^2}{a^2}$ + $\frac{x^2}{100}$ = 1 và hai đường thẳng Δ1= x+$\frac{c}{a}$ =0
Δ1= x-$\frac{c}{a}$=0 (Hình 10). Gọi d(M; Δ1), d(M; Δ2) lần lượt là khoảng cách từ M đến Δ1, Δ2. Ta có (M;Δ1)=$\left \| x+\frac{a}{e} \right \|$=
(vì e > 0 và a+ex=MF1>0a+ex=MF1>0). Suy ra
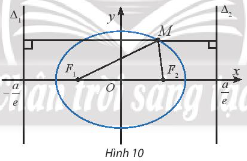
Dựa theo cách tính trên, hãy tính $\frac{MF2}{d(M,\Delta 2)}$
Có a – ex = MF2 > 0 nên a – ex > 0.
$d(M,\Delta 2)$ = $\left \| x-\frac{a}{e} \right \|$
=$\frac{\left \| ex-a \right \|}{e}$ = $\frac{a-ex}{e}$ (vì a – ex > 0).
Xem toàn bộ: Giải chuyên đề toán 10 chân trời sáng tạo bài 1 elip
Giải những bài tập khác
Giải bài tập những môn khác
Giải SGK 10 KNTT
Giải SGK 10 CTST
Giải SGK 10 Cánh diều
Giải SBT lớp 10 kết nối tri thức
Giải SBT lớp 10 chân trời sáng tạo
Giải SBT lớp 10 Cánh diều
Giải chuyên đề học tập 10 Kết nối tri thức
Giải chuyên đề học tập 10 Chân trời sáng tạo
Giải chuyên đề học tập 10 Cánh diều
Trắc nghiệm 10 Kết nối tri thức
Trắc nghiệm 10 Chân trời sáng tạo
Trắc nghiệm 10 Cánh diều
Bình luận