Giải chuyên đề toán 10 chân trời sáng tạo bài 3 Parabol
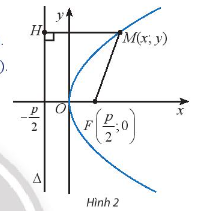
Hướng dẫn giải chuyên đề bài parabol trang 57, sách chuyên đề Toán 10 chân trời sáng tạo. Bộ sách được biên soạn nhằm góp phần phát triển năng lực vận dụng trí thức cho các em. Hi vọng, với cách hướng dẫn cụ thể và giải chi tiết học sinh sẽ nắm bài học tốt hơn.
Thêm kiến thức môn học
Từ khóa tìm kiếm: Chuyên đề toán 10 chân trời sáng tạo, giải chuyên đề toán 10 chân trời sáng tạo, giải chuyên đề toán 10 chân trời sáng tạo bài 3 parabol



Bình luận