Giải hoạt động 1 trang 39 Chuyên đề toán 10 cánh diều
I. Tính đối xứng của Elip
Hoạt động 1. Trong mặt phẳng toạ độ Oxy, ta xét elip (E) có phương trình chính tắc là $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}$, trong đó a > b > 0 (Hình 2).
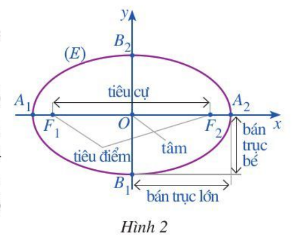
a) Tìm toạ độ hai tiêu điểm F1, F2 của (E).
b) (E) cắt trục Ox tại các điểm A1, A2 và cắt trục Oy tại các điểm B1, B2. Tìm độ dài các đoạn thẳng OA2 và OB2.
a) Tọa độ hai tiêu điểm F1, F2 của (E) là $F1(-\sqrt{a^{2}-b^{2}};0),F2(\sqrt{a^{2}-b^{2}};0)$
b)
- Vì $A_{2}$ thuộc trục Ox nên tọa độ của A2 có dạng $(x_{A2};0)$
Mà $A_{2}$ thuộc (E) nên $\frac{x_{A_{2}}^{2}}{a^{2}}+\frac{0^{2}}{b^{2}}=1\Rightarrow x_{A_{2}}^{2}=a^{2}\Rightarrow x_{A_{2}}=a$ hoặc $x_{A_{2}}=-a$
Ta thấy $A_{2}$ nằm bên phải điểm O trên trục Ox nên $x_{A_{2}}>0 \Rightarrow x_{A_{2}}=a \Rightarrow A_{2}(a;0)$. Khi đó $OA_{2}=\sqrt{(a-0)^{2}+(0-0)^{2}}=\sqrt{a^{2}}=a$ (vì a > 0)
Vậy $OA_{2}=a$
- Vì $B_{2}$ thuộc trục Oy nên tọa độ của B2 có dạng $(0;y_{B2})$
Mà $A_{2}$ thuộc (E) nên $\frac{0^{2}}{a^{2}}+\frac{y_{B_{2}}^{2}}{b^{2}}=1\Rightarrow y_{B_{2}}^{2}=b^{2}\Rightarrow y_{B_{2}}=b$ hoặc $y_{B_{2}}=-b$
Ta thấy $B_{2}$ nằm bên phải điểm O trên trục Ox nên $y_{B_{2}}>0 \Rightarrow y_{B_{2}}=b\Rightarrow B_{2}(0;b)$. Khi đó $OB_{2}=\sqrt{(0-0)^{2}+(b-0)^{2}}=\sqrt{b^{2}}=b$ (vì b > 0)
Vậy $Ob_{2}=b$
Xem toàn bộ: Giải chuyên đề toán 10 cánh diều bài 1 Elip

Bình luận