Giải bài tập 9 trang 60 SBT toán 8 tập 2 cánh diều:
Bài tập 9 trang 60 SBT toán 8 tập 2 cánh diều:
Cho tam giác ABC có ba góc nhọn, đường cao AH. Trên AH, AB, AC lần lượt lấy các điểm D, E, F sao cho $\widehat{EDC}$ = $\widehat{FDB}$ = 90°. Chứng minh; EF // BC.
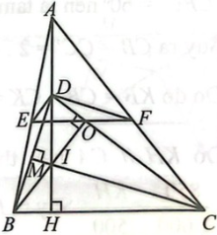
Kẻ BO ⊥ CD, CM ⊥ BD, BO cắt CM tại I, suy ra D là trực tâm của tam giác BIC hay DI ⊥ BC.
Mặt khác, AH ⊥ BC => I, D, A thẳng hàng.
Do DE // BI và DF // IC nên $\frac{AI}{AD}=\frac{AB}{AE}$ và $\frac{AI}{AD}=\frac{AC}{AF}$.
=> $\frac{AB}{AE}=\frac{AC}{AF}$
Do đó EF // BC (định lí Thalès đảo).
Giải những bài tập khác
Giải bài tập những môn khác
Giải sgk lớp 8 cánh diều
Giải SBT lớp 8 kết nối tri thức
Giải SBT lớp 8 chân trời sáng tạo
Soạn SBT lớp 8 cánh diều
Trắc nghiệm 8 Kết nối tri thức
Trắc nghiệm 8 Chân trời sáng tạo
Trắc nghiệm 8 Cánh diều
Bộ đề thi, đề kiểm tra lớp 8 chân trời sáng tạo
Giáo án lớp 8
Bình luận