Giải bài tập 8 trang 60 SBT toán 8 tập 2 cánh diều:
Bài tập 8 trang 60 SBT toán 8 tập 2 cánh diều:
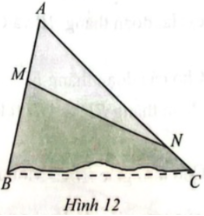
An có một mảnh bìa có dạng hình tam giác ABC nhưng bị rách. An muốn cắt bỏ phần bị rách với vết cắt là đoạn thẳng MN. Tính diện tích tứ giác MNCB theo diện tích tam giác ABC, biết $\frac{AM}{MB}=\frac{2}{3}$ và $\frac{NC}{NA}=\frac{1}{5}$ (Hình 12).
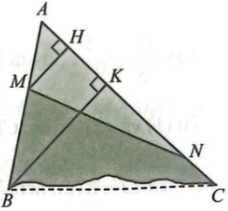
Kẻ đường cao MH của tam giác AMN và đường cao BK của tam giác ABC.
Do MH // BK nên $\frac{MH}{BK}=\frac{AM}{AB}$.
Ta có $\frac{S_{\Delta AMN}}{S_{\Delta ABC}}=\frac{(AN.MH):2}{(AC.BK):2}=\frac{AN}{AC}.\frac{AM}{AB}$ (1).
Do $\frac{AM}{MB}=\frac{2}{3}$, $\frac{NC}{NA}=\frac{1}{5}$ nên $\frac{AM}{AB}=\frac{2}{5}$, $\frac{AN}{AC}=\frac{5}{6}$ (2).
Từ (1) và (2) suy ra $\frac{S_{\Delta AMN}}{S_{\Delta ABC}}=\frac{AM}{AB}.\frac{AN}{AC}=\frac{2}{5}.\frac{5}{6}=\frac{1}{3}$
=> $S_{\Delta ABC}$ = 3$S_{\Delta AMN}$.
Từ đó dễ thấy diện tích phần bị cắt bỏ bằng $\frac{2}{3}S_{\Delta ABC}$.

Bình luận