Giải bài tập 5 trang 60 SBT toán 8 tập 2 cánh diều:
Bài tập 5 trang 60 SBT toán 8 tập 2 cánh diều:
Cho tam giác ABC vuông ở A. Vẽ ra phía ngoài tam giác đó các tam giác BAD vuông cân ở B, ACF vuông cân ở C. Gọi H là giao điểm của AB và DC, K là giao điểm của AC và BF (Hình 9).
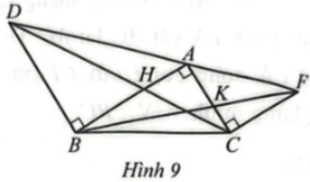
Chứng minh:
a) AH = AK;
b) AH² = AK² = HB. KC.
a) Đặt AB = c, AC = b. Vì BD // AC (cùng vuông góc với AB) và BD = AB nên
$\frac{AH}{HB}=\frac{AC}{BD}=\frac{AC}{AB}=\frac{b}{c}$
=> $\frac{AH}{AH + HB}=\frac{b}{b+c}$ hay $\frac{AH}{AB}=\frac{b}{b+c}$
Do đó AH = $\frac{bc}{b+c}$ (1).
Tương tự, ta có AB // CF (cùng vuông góc với AC) và CF = AC nên
$\frac{AK}{KC}=\frac{AB}{CF}=\frac{AB}{AC}=\frac{c}{b}$.
=> $\frac{AK}{KC+AK}=\frac{c}{b+c}$ hay $\frac{AK}{AC}=\frac{c}{b+c}$.
Do đó AK = $\frac{bc}{b+c}$ (2).
Từ (1) và (2) suy ra: AH = AK.
b) Từ $\frac{AH}{HB}=\frac{AC}{BD}=\frac{b}{c}$ và $\frac{AK}{KC}=\frac{AB}{CF}=\frac{c}{b}$
=> $\frac{AH}{HB}=\frac{KC}{AK}$.
Mà AK = AH nên $\frac{AH}{HB}=\frac{KC}{AH}$.
Do đó AH$^{2}$ = AK$^{2}$ = BH.KC.

Bình luận