Giải bài tập 30 trang 70 SBT toán 8 tập 2 cánh diều:

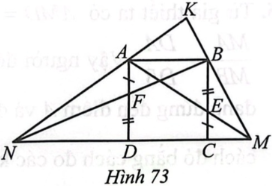
a) Vì AB // MN nên $\Delta KAB$ ᔕ $\Delta KNM$.

Vì CE // AD nên $\Delta CEM$ ᔕ $\Delta DAM$.

Vì DF // BC nên $\Delta NFD$ ᔕ $\Delta NBC$.

b) Vì $\Delta CEM$ ᔕ $\Delta BEA$ nên $\frac{CM}{BA}=\frac{CE}{BE}$ (1).

Vì $\Delta NFD$ ᔕ $\Delta BAF$ nên $\frac{AF}{FD}=\frac{BA}{DN}$ (2).

Từ (1), (2) và CE = AF, BE = DF, ta có $\frac{CM}{BA}=\frac{CE}{BE}=\frac{AF}{FD}=\frac{BA}{DN}$.

Do đó CM.DN = AB$^{2}$.

c) Ta có (CM - DN)$^{2}$ ≥ 0 => (CM + DN)$^{2}$ ≥ 4CM.DN hay CM + DN ≥ 2$\sqrt{CM.DN}$ = 2AB.

Do đó MN = DN + CD + CM ≥ 3AB (vì AB = CD).

Vậy MN có độ dài nhỏ nhất bằng 3AB. Dấu “=” xảy ra khi CM = DN  = a hay E, F lần lượt là trung điểm của BC và AD.