Giải bài tập 28 trang 70 SBT toán 8 tập 2 cánh diều:
Bài tập 28 trang 70 SBT toán 8 tập 2 cánh diều:
Quan sát Hình 28 biết $\widehat{AMN}=\widehat{ABC}$, $\widehat{BAC}=\widehat{BML}$.
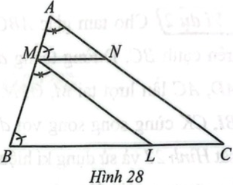
a) Chứng minh: $\Delta AMN$ ᔕ $\Delta MBL$.
b) Xác định vị trí của điểm M trên cạnh AB để chu vi tam giác AMN bằng $\frac{2}{3}$ chu vi tam giác ABC.
a) Vì $\widehat{AMN}=\widehat{ABC}$ nên MN // BC. Do đó $\Delta AMN$ ᔕ $\Delta ABC$ (1).
Vì $\widehat{BAC}=\widehat{BML}$ nên ML // AC. Do đó $\Delta MBL$ ᔕ $\Delta ABC$ (2).
Từ (1), (2) ta có $\Delta AMN$ ᔕ $\Delta MBL$.
b) Giả sử $\Delta AMN$ ᔕ $\Delta ABC$ với tỉ số đồng dạng k, ta có:
$\frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}$ = k.
=>$\frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}=\frac{AM+AN+MN}{AB+AC+BC}$ = k hay (Chu vi tam giác AMN) : (Chu vi tam giác ABC) = k.
Do đó, để chu vi tam giác AMN bằng $\frac{2}{3}$ chu vi tam giác ABC thì AM = $\frac{2}{3}$AB.
Ngược lại, dễ thấy nếu AM = $\frac{2}{3}$AB thì chu vi tam giác AMN bằng $\frac{2}{3}$ tam giác ABC.
Vậy vị trí của điểm M trên cạnh AB để chu vi tam giác AMN bằng giác ABC là AM = $\frac{2}{3}$AB.
Xem toàn bộ: Giải SBT Toán 8 Cánh diều bài 5 Tam giác đồng dạng

Bình luận