Giải bài tập 27 trang 99 SBT toán 8 tập 1 cánh diều:

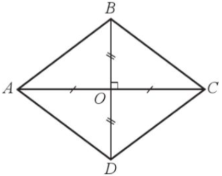
Xét hình thoi ABCD có AC = $\frac{18}{5}$ m, BD = $\frac{27}{10}$ m.

Gọi O là giao điểm của hai đường chéo AC và BD

Do ABCD là hình thoi nên AC ⊥ BD, O là trung điểm của AC và BD.

Ta tính được: OA = $\frac{AC}{2}=\frac{9}{5}$ m;

                       OB = $\frac{BD}{2}=\frac{27}{20}$ m;

Trong tam giác OAB vuông tại O, ta có: AB² = OA² + OB² = $\frac{9}{5}^{2}+ \frac{27}{20}^{2}= \frac{81}{16}$ => AB = $\frac{9}{4}$ m.

Chu vi của hình thoi ABCD là: 4. $\frac{9}{4}$ = 9 (m).

Diện tích của hình thoi ABCD là: $\frac{1}{2}.\frac{18}{5}.\frac{27}{10}=\frac{243}{50}$ (m²).