Giải bài tập 25 trang 97 SBT toán 8 tập 1 cánh diều:

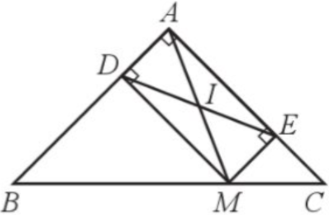
a) Tứ giác ADME có $\widehat{DAE}=\widehat{AEM}=\widehat{MDA}$ = 90° nên ADME là hình chữ nhật.

b) Do ADME là hình chữ nhật nên hai đường chéo DE và AM cắt nhau tại trung điểm của mỗi đường.

Mà I là trung điểm của DE => I là trung điểm của AM. 

Vậy ba điểm A, I, M thẳng hàng.

c) Do ADME là hình chữ nhật nên DM // AC. => $\widehat{BMD}=\widehat{ACB}$ (hai góc so le trong). 

Mà $\widehat{ABC}=\widehat{ACB}$ = 45° (vì tam giác ABC vuông cân tại A)

=> $\widehat{BMD}=\widehat{ABC}$ = 45°. Do đó tam giác BDM cân tại D. => BD = DM. 

Chu vi của hình chữ nhật ADME là: 2(AD + DM) = 2(AD + BD) = 2AB. 

Mà AB không đổi nên chu vi của tứ giác ADME không đổi. 

d) Do ADME là hình chữ nhật nên AM = DE. 

=> DE có độ dài nhỏ nhất khi AM có độ dài nhỏ nhất. 

Vậy M là hình chiếu của A trên đường thẳng BC (hình vẽ).

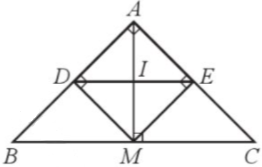
Trong tam giác ABC vuông cân tại A, ta có:

AC = AB = 2 cm và BC² = AB² + AC² = 8 => BC = $\sqrt{8}$ = 2$\sqrt{2}$ cm.

∆ABM = ∆ACM (cạnh góc vuông - góc nhọn)  => BM = CM = $\frac{BC}{2}$ = $\sqrt{2}$ cm.

Tam giác ABM vuông tại M có $\widehat{ABM}$ = 45° nên $\widehat{BAM}=\widehat{ABM}$ = 45°. 

=> tam giác ABM vuông cân tại M.  Do đó AM = BM = $\sqrt{2}$ cm. 

Vậy DE = $\sqrt{2}$ cm.