Giải bài tập 22 trang 97 SBT toán 8 tập 1 cánh diều:
Bài tập 22 trang 97 SBT toán 8 tập 1 cánh diều:
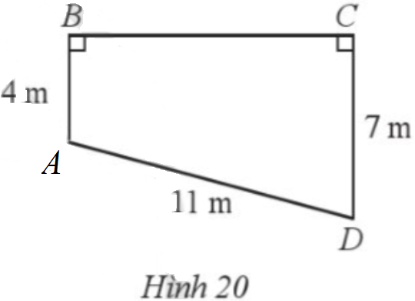
Hình 20 mô tả mặt cắt ngang tầng trệt của một ngôi nhà. Biết AB ⊥ BC, CD ⊥ BC và AB = 4 m, CD = 7 m, AD = 11 m. Tính độ dài BC (làm tròn kết quả đến hàng phần mười của mét).
Kẻ AH vuông góc với CD tại H (Hình vẽ).
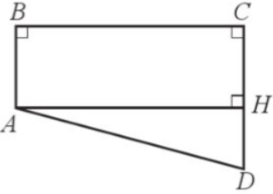
Tứ giác ABCH có $\widehat{ABC}=\widehat{BCH}=\widehat{CHA}$ = 90° nên ABCH là hình chữ nhật
=> CH = AB = 4 m.
Do đó DH = CD – CH = 3m.
Trong tam giác ADH vuông tại H, ta có: AD2 = AH2 + DH2.
=> AH2 = AD2 – DH2 = 112. Do đó AH = $\sqrt{112}$ m.
Ta có: BC = AH (vì ABCH là hình chữ nhật) nên BC = $\sqrt{112}$ ≈ 10,6 (m).
Xem toàn bộ: Giải SBT Toán 8 Cánh diều bài 5 Hình chữ nhật
Giải những bài tập khác
Giải bài tập những môn khác
Giải sgk lớp 8 cánh diều
Giải SBT lớp 8 kết nối tri thức
Giải SBT lớp 8 chân trời sáng tạo
Soạn SBT lớp 8 cánh diều
Trắc nghiệm 8 Kết nối tri thức
Trắc nghiệm 8 Chân trời sáng tạo
Trắc nghiệm 8 Cánh diều
Bộ đề thi, đề kiểm tra lớp 8 chân trời sáng tạo
Giáo án lớp 8
Bình luận