Giải bài tập 24 trang 97 SBT toán 8 tập 1 cánh diều:
Bài tập 24 trang 97 SBT toán 8 tập 1 cánh diều:
Cho tam giác ABC cân tại A có các đường trung tuyến BM, CN cắt nhau tại G. Trên tia đối của tia GB, GC lần lượt lấy các điểm D, E sao cho GD = GB, GE = GC. Tứ giác BEDC là hình gì? Vì sao?
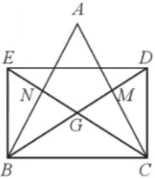
Tứ giác BEDC có hai đường chéo BD và CE cắt nhau tại trung điểm G của mỗi đường nên BEDC là hình bình hành.
Ta có: AB = AC, AM =C M, AN = BN nên BN = CM.
∆BCM = ∆CBN (c.g.c). => BM = CN.
Do G là trọng tâm của tam giác ABC nên: BG = $\frac{2}{3}$BM và CG = $\frac{2}{3}$CN.
Do đó BG = CG. Mà G là trung điểm của BD và CE => BD = CE.
Hình bình hành BEDC có BD = CE nên BEDC là hình chữ nhật.
Xem toàn bộ: Giải SBT Toán 8 Cánh diều bài 5 Hình chữ nhật
Giải những bài tập khác
Giải bài tập những môn khác
Giải sgk lớp 8 cánh diều
Giải SBT lớp 8 kết nối tri thức
Giải SBT lớp 8 chân trời sáng tạo
Soạn SBT lớp 8 cánh diều
Trắc nghiệm 8 Kết nối tri thức
Trắc nghiệm 8 Chân trời sáng tạo
Trắc nghiệm 8 Cánh diều
Bộ đề thi, đề kiểm tra lớp 8 chân trời sáng tạo
Giáo án lớp 8
Bình luận