Giải bài tập 25 trang 68 SBT toán 8 tập 2 cánh diều:
Bài tập 25 trang 68 SBT toán 8 tập 2 cánh diều:
Một người đứng ở vị trí M trên cây cầu bắc qua con kênh quan sát ba điểm thẳng hàng A, B, D lần lượt là chân hai cột đèn trồng ở bờ kênh và chân cầu (Hình 26). Người đó nhận thấy góc nhìn đến hai điểm A, D thì bằng góc nhìn đến hai điểm B, D, tức là $\widehat{AMD}=\widehat{BMD}$. Người đó muốn ước lượng tỉ số khoảng cách từ vị trí M đang đứng đến điểm A và đến điểm B mà không cần phải đo trực tiếp hai khoảng cách đó. Hỏi có thể ước lượng tỉ số đó được hay không?
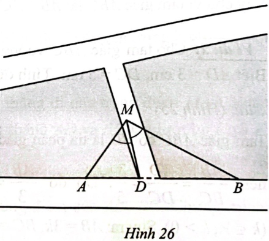
Từ giả thiết ta có $\widehat{AMD}=\widehat{BMD}$, suy ra MD là phân giác của góc AMB. Do đó $\frac{MA}{MB}=\frac{DA}{DB}$.
Vậy người đó có thể ước lượng được tỉ số khoảng cách từ vị trí M đang đứng đến điểm A và đến điểm B mà không cần phải đo trực tiếp hai khoảng cách đó bằng cách đo các khoảng cách DA, DB và tính $\frac{DA}{DB}$.

Bình luận