Giải bài tập 24 trang 68 SBT toán 8 tập 2 cánh diều:

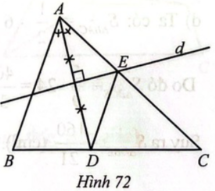
Đường trung trực của đoạn AD cắt AC tại E nên tam giác AED cân tại E. Do đó $\widehat{EDA}=\widehat{EAD}$. 

Mà $\widehat{EAD}=\widehat{DAB}$ (AD là đường phân giác của tam giác ABC) => $\widehat{EDA}=\widehat{DAB}$.

Lại có hai góc $\widehat{EDA},\widehat{DAB}$ ở vị trí so le trong nên DE // AB.  Do đó: $\frac{ED}{AB}=\frac{DC}{BC}$

Mặt khác do $\frac{DC}{DB}=\frac{AC}{AB}=\frac{9}{6}=\frac{3}{2}$ nên $\frac{DC}{DC+DB}=\frac{3}{3+2}=\frac{3}{5}$ 

=> $\frac{DC}{BC}=\frac{3}{5}$

=> $\frac{ED}{AB}=\frac{DC}{BC}=\frac{3}{5}$.

Vậy ED = $\frac{3}{5}$.AB = $\frac{3}{5}$.6 = 3,6 (cm).