Giải bài tập 21 trang 67 SBT toán 8 tập 2 cánh diều:

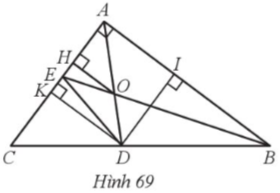
a) Tam giác vuông ABC vuông tại A nên theo định lí Pythagore, ta có: BC$^{2}$ = AC$^{2}$ + AB$^{2}$ = 100, suy ra BC = 10 (cm).

Vì BE là phân giác nên: $\frac{AE}{EC}=\frac{AB}{BC}=\frac{8}{10}=\frac{4}{5}$

Suy ra $\frac{AE}{4}=\frac{EC}{5}=\frac{AE+EC}{4+5}=\frac{6}{9}=\frac{2}{3}$.

Vậy AE = $\frac{8}{3}$ cm; EC = $\frac{10}{3}$ cm.

b) Kẻ OH vuông góc với AC tại H, OH ⊥ AC, BA ⊥ AC nên OH // AB.

=> $\frac{OH}{AB}=\frac{OE}{EB}$ (1).

Tam giác AEB có AO là phân giác nên $\frac{EO}{OB}=\frac{AE}{AB}=\frac{1}{3}$.

=> $\frac{EO}{EB}=\frac{1}{4}$ (2).

Từ (1) và (2) ta có $\frac{OH}{AB}=\frac{1}{4}$ => OH = 2 cm.

c) Kẻ DK ⊥ AC, DI ⊥ AB. Khi đó, tứ giác AKDI có ba góc vuông và đường chéo AD là đường phân giác của góc KAI nên tứ giác AKDI là hình vuông. Suy ra DK = DI. 

Ta có $S_{\Delta ABC}=S_{\Delta ADC}+S_{\Delta ADB}$ nên $\frac{AC.AB}{2}=\frac{AC.DK}{2}+\frac{AB.DI}{2}$ 

hay AC.AB = AC.DK + AB.DI = (AB + AC).DK (do DK = DI).

Từ đó, ta có DK = $\frac{AB.AC}{AB+AC}=\frac{8.6}{8+6}=\frac{24}{7}$.

Tứ giác AKDI là hình vuông nên AD = DK$\sqrt{2}$ = $\frac{24\sqrt{2}}{7}$ ≈ 4,8 (cm).

d) Ta có: $S_{\Delta BAC}=\frac{1}{2}$.6.8 = 24 (cm$^{2}$).

=> $\frac{S_{\Delta BCE}}{S_{\Delta BAC}}=\frac{EC}{AC}=\frac{10}{3}:6=\frac{5}{9}$.

Do đó $S_{\Delta BCE}=\frac{5}{9}.24=\frac{40}{3}$ (cm$^{2}$).

Tương tự: $\frac{S_{\Delta DBE}}{S_{\Delta BEC}}=\frac{DB}{BC}=\frac{4}{7}$.

=> $S_{\Delta DBE}=\frac{4}{7}.\frac{40}{3}=\frac{160}{21}$ (cm$^{2}$).

Mà $\frac{S_{\Delta DOE}}{S_{\Delta DBE}}=\frac{OE}{BE}=\frac{1}{4}$.

=> $S_{\Delta DOE}=\frac{1}{4}.\frac{160}{21}=\frac{40}{21}$ (cm$^{2}$).