Giải bài tập 21 trang 79 SBT toán 8 tập 1 cánh diều:
Bài tập 21 trang 79 SBT toán 8 tập 1 cánh diều:
Cho hình chóp tứ giác đều S.ABCD có chiều cao SH. Gọi E, F lần lượt là trung điểm của AB, CD. Kẻ EK vuông góc với SF tại K (Hình 14). Biết AB = EF = 13cm, SH = EK. Tính tổng diện tích các mặt của hình chóp tứ giác đều đó.
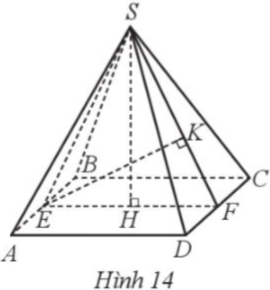
Ta có diện tích của tam giác SEF bằng:
$\frac{1}{2}.SH.EF=\frac{1}{2}.EK.SF$.
Mà SH = EK => SF = EF = 13 cm.
Diện tích xung quanh của hình chóp tứ giác đều S.ABCD là
$\frac{1}{2} $.(13. 4). 13 = 338 (cm2).
Diện tích đáy của hình chóp tứ giác đều S.ABCD là
132 = 169 (cm2).
Tổng diện tích các mặt của hình chóp tứ giác đều S.ABCD là:
338 + 169 = 507 (cm2).
Xem toàn bộ: Giải SBT Toán 8 Cánh diều bài Bài tập cuối chương IV
Giải những bài tập khác
Giải bài tập những môn khác
Giải sgk lớp 8 cánh diều
Giải SBT lớp 8 kết nối tri thức
Giải SBT lớp 8 chân trời sáng tạo
Soạn SBT lớp 8 cánh diều
Trắc nghiệm 8 Kết nối tri thức
Trắc nghiệm 8 Chân trời sáng tạo
Trắc nghiệm 8 Cánh diều
Bộ đề thi, đề kiểm tra lớp 8 chân trời sáng tạo
Giáo án lớp 8
Bình luận