Giải bài tập 20 trang 95 SBT toán 8 tập 1 cánh diều:

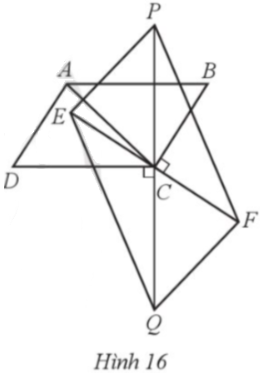
a) Tứ giác EPFQ có hai đường chéo EF và PQ cắt nhau tại trung điểm C của mỗi đường nên EPFQ là hình bình hành.

b*) Gọi H là giao điểm của AC và EP, K là giao điểm của AB và PQ (Hình vẽ).

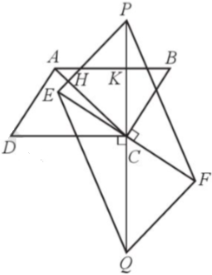
Do ABCD là hình bình hành nên AB // CD, AD = BC, $\widehat{B}=\widehat{D}$.

Vì AB // CD nên $\widehat{BKC}=\widehat{DCK}$ = 90° (hai góc so le trong). 

=> tam giác BCK vuông tại K. 

Do đó $\widehat{B}+\widehat{BCK}$ = 90°.

Mà $\widehat{B}=\widehat{D}$ => $\widehat{D}+\widehat{BCK}$ = 90°.

Mặt khác, ta có $\widehat{ECP}+\widehat{BCK}$ = $\widehat{BCE}$ = 90° nên $\widehat{D}=\widehat{ECP}$.

Xét hai tam giác ACD và EPC, ta có:

AD = EC (vì cùng bằng BC); $\widehat{D}=\widehat{ECP}$; CD = PC.

=> ∆ACD = ∆EPC (c.g.c). Do đó $\widehat{ACD}=\widehat{EPC}$ (hai góc tương ứng) hay $\widehat{ACD}=\widehat{HPC}$. 

Mà $\widehat{ACD}+\widehat{PCH}$ = $\widehat{DCP}$ = 90°

=> $\widehat{HPC}+\widehat{PCH}$ =90°. 

Xét tam giác CPH, ta có: $\widehat{CHP}+\widehat{HPC}+\widehat{PCH}$ =180°.

Suy ra $\widehat{CHP}$ + 90° = 180° hay $\widehat{CHP}$ = 90°. 

Vậy AC ⊥ EP.