Giải bài tập 20 trang 66 SBT toán 8 tập 2 cánh diều:

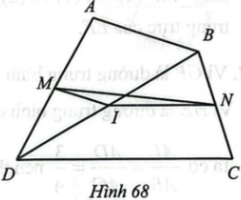
Lấy I là trung điểm của BD. Khi đó, ta có MI, NI lần lượt là các đường trung bình của tam giác ABD và BDC nên MI = $\frac{AB}{2}$, NI = $\frac{CD}{2}$.

Do đó MI + NI = $\frac{AB+CD}{2}$ (1).

- Nếu I không thuộc MN ta có MN < MI + NI (bất đẳng thức tam giác).

- Nếu I thuộc MN ta có MN = MI+NI.

Tức là, ta luôn có MN ≤ MI + NI (2). 

Từ (1), (2) suy ra MN ≤ $\frac{AB+DC}{2}$.

Dấu đẳng thức xảy ra khi I thuộc MN, khi đó AB // CD.