Giải Bài tập 17 trang 60 sgk Toán 8 tập 2 Chân trời

a) Xét tam giác ABH có $\widehat{AHB}=90^{\circ}$ suy ra $\widehat{HAB}+\widehat{ABH}=90$ (1)

Lại có: $\widehat{HAK}=90$ suy ra $\widehat{HAB}+\widehat{BAK}=90$ (2)

Từ (1) (2) suy ra $\widehat{ABH}=\widehat{BAK}$ (3) mà hai góc này ở vị trí so le trong nên HB // AK

Do đó $\widehat{KAC }=\widehat{BDA}$ (hai góc đồng vị)  (4)

Tam giác ABD có AD = AB suy ra tam giác ABD cân tại A nên $\widehat{BDA}=\widehat{ABH}$ (5)

Từ (3) (4) (5) suy ra $\widehat{BAK}=\widehat{KAC}$ 

Vậy AK là phân giác góc $\widehat{BAC}$

b)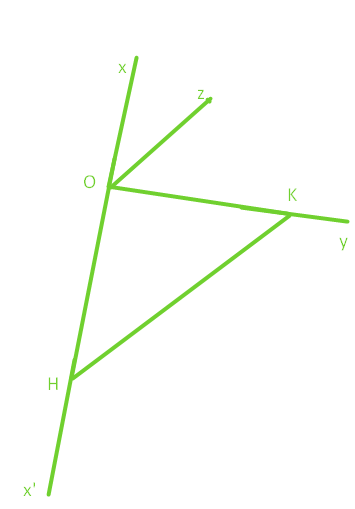 

Giả sử để vẽ tia phân giác giác của góc xOy ta làm như sau:

- Ox' là tia đối của tia Ox

- Trên Ox' và Oy lần lượt lấy H và K sao cho OH = OK, nối H với K

- Từ O kẻ tia Oz song song với HK

- Ta được Oz là tia phân giác góc xOy