Giải Bài tập 15 trang 60 sgk Toán 8 tập 2 Chân trời

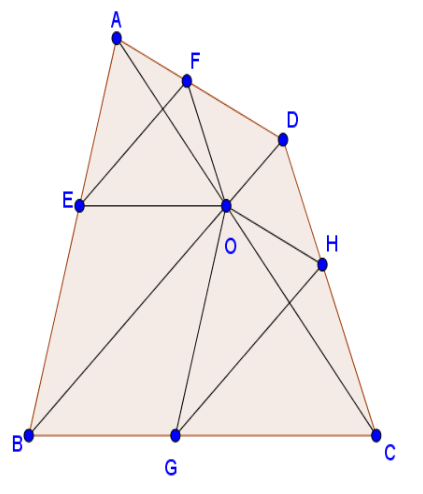
a) Tam giác ABC có OE // BC (gt) suy ra $\frac{AE}{AB}=\frac{AO}{AC}$ (theo định lí Thales) (1)

Tam giác ADC có OF // CD (gt) suy ra $\frac{AO}{AC}=\frac{AF}{AD}$ (theo định lí Thales) (2)

Từ (1) và (2) suy ra $\frac{AE}{AB}=\frac{AF}{AD}$

Tam giác ADB có $\frac{AE}{AB}=\frac{AF}{FD}$ suy ra EF // BD (theo định lý Thales đảo)

b) Tam giác ABC có OG // AB (gt) suy ra $\frac{CG}{BG}=\frac{CO}{AO}$ (theo định lí Thales) (3)

Tam giác ACD có OH // AD (gt) suy ra $\frac{CO}{AO}=\frac{CH}{DH}$ (theo định lí Thales) (4)

Từ (3) (4) suy ra $\frac{CG}{BG}=\frac{CH}{DH}$ suy ra CG x DH = BG x CH