Giải bài tập 14 trang 92 SBT toán 8 tập 1 cánh diều:

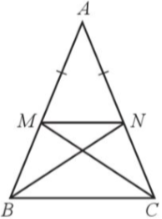
a) Vì hai tam giác AMN và ABC đều cân tại A nên

$\widehat{AMN}=\widehat{ABC}$ (cùng bằng $\frac{180^{o}-\widehat{A}}{2}$).

Mà $\widehat{AMN}$ và $\widehat{ABC}$ nằm ở vị trí đồng vị => MN // BC. 

Tứ giác BMNC có MN // BC và $\widehat{MBC}=\widehat{NCB}$ nên BMNC là hình thang cân.

b) Do BM = MN nên tam giác MBN cân tại M 

=> $\widehat{MNB}=\widehat{MBN}$ (hai góc so le trong)

=> $\widehat{MBN}=\widehat{NBC}$ 

Do đó, BN là tia phân giác của góc ABC.

Tương tự, ta cũng chứng minh được CM là tia phân giác của góc ACB.

Dễ thấy, nếu các điểm M, N được xác định sao cho BN, CM lần lượt là tia phân giác của góc ABC, ACB thì BN = MN = CN.

Vậy M là giao điểm của AB và tia phân giác của góc ACB, N là giao điểm của AC và tia phân giác của góc ABC thì BN = MN = CN.