Giải bài tập 11 trang 92 SBT toán 8 tập 1 cánh diều:

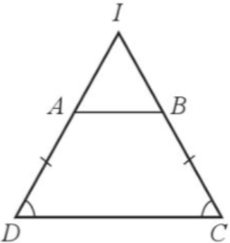
Gọi I là giao điểm của AD và BC. 

Do $\widehat{C}=\widehat{D}$ nên tam giác ICD cân tại I =>  ID = IC. 

Mà AD = BC => IA = IB. 

Do đó, tam giác IAB cân tai I.

Vì hai tam giác IAB và ICD đều cân tại I nên

$\widehat{IAB}=\widehat{D}$ (cùng bằng $\frac{180^{o}-\widehat{I}}{2}$).

Mà $\widehat{IAB}$ và $\widehat{D}$ nằm ở vị trí đồng vị, suy ra AB // CD.

Tứ giác ABCD có AB // CD và $\widehat{C}=\widehat{D}$ nên ABCD là hình thang cân.